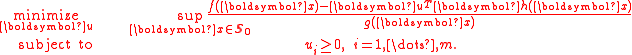Fractional programming
Encyclopedia
In mathematical optimization, fractional programming is a generalization of linear-fractional programming
. The objective function in a fractional program is a ratio of two functions that are in general nonlinear. The ratio to be optimized often describes some kind of efficiency of a system.
 be real-valued function
be real-valued function
s defined on a set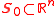 . Let
. Let 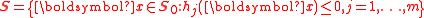 . The nonlinear program
. The nonlinear program
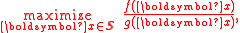
where on
on 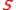 , is called a fractional program.
, is called a fractional program.
is called a concave fractional program. If g is affine, f does not have to be restricted in sign. The linear fractional program is a special case of a concave fractional program where all functions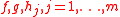 are affine.
are affine.
 is semistrictly quasiconcave on S. If f and g are differentiable, then q is pseudoconcave. In a linear fractional program, the objective function is pseudolinear.
is semistrictly quasiconcave on S. If f and g are differentiable, then q is pseudoconcave. In a linear fractional program, the objective function is pseudolinear.
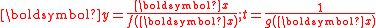 , any concave fractional program can be transformed to the equivalent parameter-free concave program
, any concave fractional program can be transformed to the equivalent parameter-free concave program
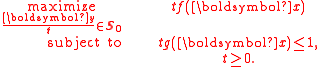
If g is affine, the first constraint is changed to .
.
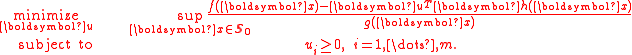
Linear-fractional programming
In mathematical optimization, linear-fractional programming is a generalization of linear programming . Whereas the objective function in linear programs are linear functions, the objective function in a linear-fractional program is a ratio of two linear functions...
. The objective function in a fractional program is a ratio of two functions that are in general nonlinear. The ratio to be optimized often describes some kind of efficiency of a system.
Definition
Let be real-valued function
be real-valued functionReal-valued function
In mathematics, a real-valued function is a function that associates to every element of the domain a real number in the image....
s defined on a set
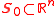 . Let
. Let 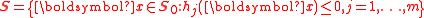 . The nonlinear program
. The nonlinear programNonlinear programming
In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
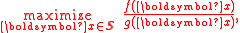
where
 on
on 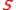 , is called a fractional program.
, is called a fractional program.Concave fractional programs
A fractional program in which f is nonnegative and concave, g is positive and convex, and S is a convex setConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
is called a concave fractional program. If g is affine, f does not have to be restricted in sign. The linear fractional program is a special case of a concave fractional program where all functions
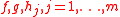 are affine.
are affine.Properties
The function is semistrictly quasiconcave on S. If f and g are differentiable, then q is pseudoconcave. In a linear fractional program, the objective function is pseudolinear.
is semistrictly quasiconcave on S. If f and g are differentiable, then q is pseudoconcave. In a linear fractional program, the objective function is pseudolinear.Transformation to a concave program
By the transformation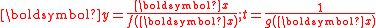 , any concave fractional program can be transformed to the equivalent parameter-free concave program
, any concave fractional program can be transformed to the equivalent parameter-free concave program 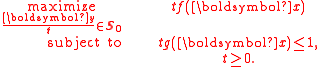
If g is affine, the first constraint is changed to
 .
.Duality
The Lagrangean dual of the equivalent concave program is