Free deconvolution
Encyclopedia
Free convolution is the free probability
analog of the classical notion of convolution
of probability measures. Due to the non-commutative nature of free probability theory, one has to talk separately about additive and multiplicative free convolution, which arise from addition and multiplication of free random variables (see below; in the classical case, what would be the analog of free multiplicative convolution can be reduced to additive convolution by passing to logarithms of random variables).
The notion of free convolution was introduced by Voiculescu in early 80s in the papers and .
and 
be two probability measures on the real line, and assume that 
is a random variable with law 
and 
is a random variable with law 
. Assume finally that 
and 
are freely independent
. Then the free additive convolution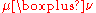
is the law of 
.
In many cases, it is possible to compute the probability measure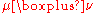
explicitly by using complex-analytic techniques and the R-transform of the measures 
and 
.
and 
be two probability measures on the interval 
, and assume that 
is a random variable with law 
and 
is a random variable with law 
. Assume finally that 
and 
are freely independent
. Then the free multiplicative convolution
is the law of 
(or, equivalently, the law of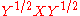 
.
A similar definition can be made in the case of laws
supported on the unit circle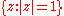 
.
Explicit computations of multiplicative free convolution can be carried out using complex-analytic techniques and the S-transform.
Through its applications to random matrices, free convolution has some strong connections with other works on G-estimation of Girko.
The applications in wireless communications, finance
and biology
have provided a useful framework when the number of observations is of the same order as the dimensions of the system.
Free probability
Free probability is a mathematical theory that studies non-commutative random variables. The "freeness" or free independence property is the analogue of the classical notion of independence, and it is connected with free products....
analog of the classical notion of convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of probability measures. Due to the non-commutative nature of free probability theory, one has to talk separately about additive and multiplicative free convolution, which arise from addition and multiplication of free random variables (see below; in the classical case, what would be the analog of free multiplicative convolution can be reduced to additive convolution by passing to logarithms of random variables).
The notion of free convolution was introduced by Voiculescu in early 80s in the papers and .
Free additive convolution
Let and be two probability measures on the real line, and assume that is a random variable with law and is a random variable with law . Assume finally that and are freely independentFree independence
In the mathematical theory of free probability, the notion of free independence was introduced by Dan Voiculescu. The definition of free independence is parallel to the classical definition of independence, except that the role of Cartesian products of measure spaces is played by the notion of a...
. Then the free additive convolution
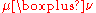is the law of .In many cases, it is possible to compute the probability measure
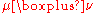explicitly by using complex-analytic techniques and the R-transform of the measures and .Free multiplicative convolution
Let and be two probability measures on the interval , and assume that is a random variable with law and is a random variable with law . Assume finally that and are freely independentFree independence
In the mathematical theory of free probability, the notion of free independence was introduced by Dan Voiculescu. The definition of free independence is parallel to the classical definition of independence, except that the role of Cartesian products of measure spaces is played by the notion of a...
. Then the free multiplicative convolution
is the law of (or, equivalently, the law of 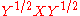.A similar definition can be made in the case of laws
supported on the unit circle 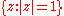.Explicit computations of multiplicative free convolution can be carried out using complex-analytic techniques and the S-transform.
Applications of free convolution
- Free convolution can be used to give a proof of the free central limit theorem.
- Free convolution can be used to compute the laws and spectra of sums or products of random variables which are free. Such examples include: random walkRandom walkA random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
operators on free groups (Kesten measures); and asymptotic distribution of eigenvalues of sums or products of independent random matricesRandom matrixIn probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...
.
Through its applications to random matrices, free convolution has some strong connections with other works on G-estimation of Girko.
The applications in wireless communications, finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
and biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
have provided a useful framework when the number of observations is of the same order as the dimensions of the system.