Frobenius theorem (real division algebras)
Encyclopedia
In mathematics
, more specifically in abstract algebra
, the Frobenius theorem, proved by Ferdinand Georg Frobenius
in 1877, characterizes the finite-dimensional associative
division algebra
s over the real number
s. According to the theorem, every such algebra is isomorphic to one of the following:
These algebras have dimensions 1, 2, and 4, respectively. Of these three algebras, the real and complex numbers are commutative, but the quaternions are not.
This theorem is closely related to Hurwitz's theorem, which states that the only normed division algebra
s over the real numbers are R, C, H, and the (non-associative) algebra O of octonions.
and the fundamental theorem of algebra
.
We can consider D as a finite-dimensional R-vector space
. Any element d of D defines an endomorphism
of D by left-multiplication and we will identify d with that endomorphism. Therefore we can speak about the trace
of d, the characteristic
and minimal polynomial
s. Also, we identify the real multiples of 1 with R. When we write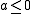
for an element a of D, we tacitly assume that a is contained in R.
The key to the argument is the following
Claim: The set V of all elements a of D such that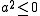
is a vector subspace of D of codimension
1.
To see that, we pick an a ∈ D. Let m be the dimension of D as an R-vector space. Let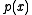
be the characteristic polynomial of a. By the fundamental theorem of algebra, we can write
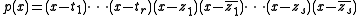
for some real ti and (non-real) complex numbers zj. We have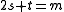
. The polynomials 
are irreducible
over R. By the Cayley–Hamilton theorem, p(a) = 0 and because D is a division algebra, it follows that either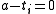
for some i or that 
, 
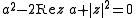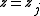for some j. The first case implies that a ∈ R. In the second case, it follows that 
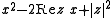is the minimal polynomial of a. Because p(x) has the same complex roots as the minimal polynomial and because it is real it follows that
and m=2k. The coefficient of
in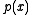 
is the trace of a (up to sign). Therefore we read from that equation: the trace of a is zero if and only if 
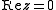, that is 
.
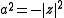Therefore V is the subset of all a with tr a = 0. In particular, it is a vector subspace (!). Moreover, V has codimension 1 since it is the kernel of a (nonzero) linear form. Also note that D is the direct sum of R and V (as vector spaces). Therefore, V generates D as an algebra.
Define now for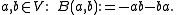
Because of the identity 
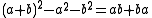, it follows that 
is real and since 
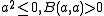if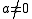 
. Thus B is a positive definite symmetric bilinear form
, in other words, an inner product on V.
Let W be a subspace of V which generated D as an algebra and which is minimal with respect to that property. Let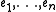
be an orthonormal basis
of W. These elements satisfy the following relations:
If n = 0, then D is isomorphic to R.
If n = 1, then D is generated by 1 and e1 subject to the relation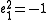
. Hence it is isomorphic to C.
If n = 2, it has been shown above that D is generated by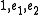
subject to the relations 
and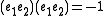 
. These are precisely the relations for H.
If n > 2, the D cannot be a division algebra. Assume that n > 2. Put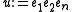
. It is easy to see that 
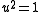(this only works if n > 2). Therefore 
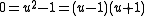implies that u= ±1 (because D is still assumed to be a division algebra). But if u= ±1, then 
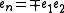and so 
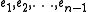generates D. This contradicts the minimality of W.
Remark: The fact that D is generated by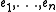
subject to above relation can be interpreted as the statement that D is the Clifford algebra
of Rn. The last step shows that the only real Clifford algebras which are division algebras are Cl0, Cl1 and Cl2.
Remark: As a consequence, the only commutative division algebras are R and C. Also note that H is not a C-algebra. If it were, then the center of H has to contain C, but the center of H is R. Therefore, the only division algebra over C is C itself.
, locally compact
division ring
, then either D = R, or D = C, or D = H.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the Frobenius theorem, proved by Ferdinand Georg Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
in 1877, characterizes the finite-dimensional associative
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
s over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. According to the theorem, every such algebra is isomorphic to one of the following:
- R (the real numbers)
- C (the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s) - H (the quaternions).
These algebras have dimensions 1, 2, and 4, respectively. Of these three algebras, the real and complex numbers are commutative, but the quaternions are not.
This theorem is closely related to Hurwitz's theorem, which states that the only normed division algebra
Normed division algebra
In mathematics, a normed division algebra A is a division algebra over the real or complex numbers which is also a normed vector space, with norm || · || satisfying the following property:\|xy\| = \|x\| \|y\| for all x and y in A....
s over the real numbers are R, C, H, and the (non-associative) algebra O of octonions.
Proof
The main ingredients for the following proof are the Cayley–Hamilton theoremCayley–Hamilton theorem
In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....
and the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
.
We can consider D as a finite-dimensional R-vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. Any element d of D defines an endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
of D by left-multiplication and we will identify d with that endomorphism. Therefore we can speak about the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of d, the characteristic
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
and minimal polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s. Also, we identify the real multiples of 1 with R. When we write
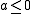for an element a of D, we tacitly assume that a is contained in R.The key to the argument is the following
Claim: The set V of all elements a of D such that
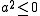is a vector subspace of D of codimensionCodimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
1.
To see that, we pick an a ∈ D. Let m be the dimension of D as an R-vector space. Let
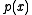be the characteristic polynomial of a. By the fundamental theorem of algebra, we can write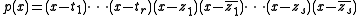for some real ti and (non-real) complex numbers zj. We have
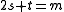. The polynomials are irreducibleIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over R. By the Cayley–Hamilton theorem, p(a) = 0 and because D is a division algebra, it follows that either
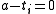for some i or that 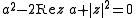, 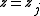for some j. The first case implies that a ∈ R. In the second case, it follows that 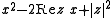is the minimal polynomial of a. Because p(x) has the same complex roots as the minimal polynomial and because it is real it follows thatand m=2k. The coefficient of
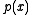in is the trace of a (up to sign). Therefore we read from that equation: the trace of a is zero if and only if 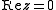, that is 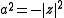.Therefore V is the subset of all a with tr a = 0. In particular, it is a vector subspace (!). Moreover, V has codimension 1 since it is the kernel of a (nonzero) linear form. Also note that D is the direct sum of R and V (as vector spaces). Therefore, V generates D as an algebra.
Define now for
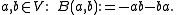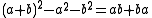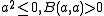Because of the identity , it follows that is real and since if 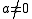. Thus B is a positive definite symmetric bilinear formSymmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
, in other words, an inner product on V.
Let W be a subspace of V which generated D as an algebra and which is minimal with respect to that property. Let
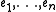be an orthonormal basisOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of W. These elements satisfy the following relations:
If n = 0, then D is isomorphic to R.
If n = 1, then D is generated by 1 and e1 subject to the relation
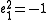. Hence it is isomorphic to C.If n = 2, it has been shown above that D is generated by
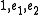subject to the relations and 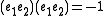. These are precisely the relations for H.If n > 2, the D cannot be a division algebra. Assume that n > 2. Put
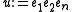. It is easy to see that 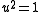(this only works if n > 2). Therefore 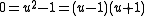implies that u= ±1 (because D is still assumed to be a division algebra). But if u= ±1, then 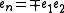and so 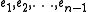generates D. This contradicts the minimality of W.Remark: The fact that D is generated by
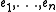subject to above relation can be interpreted as the statement that D is the Clifford algebraClifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
of Rn. The last step shows that the only real Clifford algebras which are division algebras are Cl0, Cl1 and Cl2.
Remark: As a consequence, the only commutative division algebras are R and C. Also note that H is not a C-algebra. If it were, then the center of H has to contain C, but the center of H is R. Therefore, the only division algebra over C is C itself.
Pontryagin variant
If D is a connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
division ring
Topological ring
In mathematics, a topological ring is a ring R which is also a topological space such that both the addition and the multiplication are continuous as mapswhere R × R carries the product topology.- General comments :...
, then either D = R, or D = C, or D = H.