
Frozen orbit
Encyclopedia
For most spacecraft missions the "perturbing forces" caused by the oblateness of the Earth, the gravitational attraction from Sun/Moon, the solar radiation pressure and the air drag must be counteracted by orbit maneuvers to keep the spacecraft in the desired orbit. For a geostationary spacecraft
one needs for example orbit correction maneuvers in the order of 40–50 m/s per year to counteract the gravitational force from Sun/Moon which perturbs the orbital plane moving it away from the equatorial plane of the Earth.
For Sun-synchronous spacecraft
the precession of the orbital plane around the polar axis of the Earth caused by the oblateness of the Earth is on the contrary utilized to the benefit of the mission. For this a circular or almost circular orbit typically in the altitude range 600–900 km with the matching inclination in the range 97.8-99.0 deg is used, the inclination being selected such that the precession rate of the orbital plane is equal to the mean rate of the Earth in its orbit around the Sun. In this way is achieved that Sun illumination of any area below the spacecraft is roughly the same for the different over-flights (the north-bound overflights and the south-bound overflights, respectively) what is an advantage for many Earth observation missions.
But the perturbing force caused by the oblateness of the Earth will in general perturb not only the orbital plane but also the eccentricity vector of the orbit. There exists, however, an almost-circular orbit for which there are no secular/long periodic perturbations of the eccentricity vector, only periodic perturbations with period equal to the orbital period. Such an orbit is then perfectly periodic (except for the orbital plane precession) and it is therefore called a "frozen orbit". Such an orbit is often the preferred choice for an Earth observation mission where repeated observations of the same area of the Earth should be made under as constant observation conditions as possible.
The Earth observation satellite
s ERS-1, ERS-2
and Envisat
are all operated in Sun-synchronous "frozen" orbits
for artificial satellites of Dirk Brouwer
made under contract with NASA
and published in 1959.
This analysis can be carried out as follows:
In the article Orbital perturbation analysis (spacecraft)
the secular perturbation of the orbital pole from the
from the  term is shown to be
term is shown to be
Geostationary orbit
A geostationary orbit is a geosynchronous orbit directly above the Earth's equator , with a period equal to the Earth's rotational period and an orbital eccentricity of approximately zero. An object in a geostationary orbit appears motionless, at a fixed position in the sky, to ground observers...
one needs for example orbit correction maneuvers in the order of 40–50 m/s per year to counteract the gravitational force from Sun/Moon which perturbs the orbital plane moving it away from the equatorial plane of the Earth.
For Sun-synchronous spacecraft
Sun-synchronous orbit
A Sun-synchronous orbit is a geocentric orbit which combines altitude and inclination in such a way that an object on that orbit ascends or descends over any given point of the Earth's surface at the same local mean solar time. The surface illumination angle will be nearly the same every time...
the precession of the orbital plane around the polar axis of the Earth caused by the oblateness of the Earth is on the contrary utilized to the benefit of the mission. For this a circular or almost circular orbit typically in the altitude range 600–900 km with the matching inclination in the range 97.8-99.0 deg is used, the inclination being selected such that the precession rate of the orbital plane is equal to the mean rate of the Earth in its orbit around the Sun. In this way is achieved that Sun illumination of any area below the spacecraft is roughly the same for the different over-flights (the north-bound overflights and the south-bound overflights, respectively) what is an advantage for many Earth observation missions.
But the perturbing force caused by the oblateness of the Earth will in general perturb not only the orbital plane but also the eccentricity vector of the orbit. There exists, however, an almost-circular orbit for which there are no secular/long periodic perturbations of the eccentricity vector, only periodic perturbations with period equal to the orbital period. Such an orbit is then perfectly periodic (except for the orbital plane precession) and it is therefore called a "frozen orbit". Such an orbit is often the preferred choice for an Earth observation mission where repeated observations of the same area of the Earth should be made under as constant observation conditions as possible.
The Earth observation satellite
Earth observation satellite
Earth observation satellites are satellites specifically designed to observe Earth from orbit, similar to reconnaissance satellites but intended for non-military uses such as environmental monitoring, meteorology, map making etc....
s ERS-1, ERS-2
European Remote-Sensing Satellite
European remote sensing satellite was the European Space Agency's first Earth-observing satellite. It was launched on July 17, 1991 into a Sun-synchronous polar orbit at a height of 782–785 km.-Instruments:...
and Envisat
Envisat
Envisat is an Earth-observing satellite. It was launched on 1 March 2002 aboard an Ariane 5 from the Guyana Space Centre in Kourou, French Guyana into a Sun synchronous polar orbit at an altitude of...
are all operated in Sun-synchronous "frozen" orbits
Classical theory
The classical theory of "frozen orbits" is essentially based on the analytical perturbation analysisOrbital perturbation analysis (spacecraft)
Isaac Newton in his Philosophiæ Naturalis Principia Mathematica demonstrated that the gravitational force between two mass points is inversely proportional to the square of the distance between the points and fully solved corresponding "two-body problem" demonstrating that radius vector between the...
for artificial satellites of Dirk Brouwer
Dirk Brouwer
Dirk Brouwer was a Dutch-American astronomer.He received his Ph.D. in 1927 at Leiden University in the Netherlands and then went to Yale University...
made under contract with NASA
NASA
The National Aeronautics and Space Administration is the agency of the United States government that is responsible for the nation's civilian space program and for aeronautics and aerospace research...
and published in 1959.
This analysis can be carried out as follows:
In the article Orbital perturbation analysis (spacecraft)
Orbital perturbation analysis (spacecraft)
Isaac Newton in his Philosophiæ Naturalis Principia Mathematica demonstrated that the gravitational force between two mass points is inversely proportional to the square of the distance between the points and fully solved corresponding "two-body problem" demonstrating that radius vector between the...
the secular perturbation of the orbital pole
 from the
from the  term is shown to be
term is shown to be
-
what in terms of orbital elements is expressed as
-
-
Making the analogue analysis for the term, one gets
term, one gets
-
what in terms of orbital elements is expressed as
-
-
In the same article the secular perturbation of the components of the eccentricity vectorKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
caused by the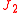 is shown to be:
is shown to be:
-
where:
- The first term is the in-plane perturbation of the eccentricity vector caused by the in-plane component of the perturbing force
- The second term is the effect of the new position of the ascending node in the new orbital plane, the orbital plane being perturbed by the out-of-plane force component
Making the analogue analysis for the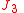 term one gets for the first term, i.e. for the perturbation of the eccentricity vector from the in-plane force component
term one gets for the first term, i.e. for the perturbation of the eccentricity vector from the in-plane force component
-
For inclinations in the range 97.8–99.0 deg, the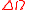 value given by is much smaller than the value given by and can be ignored. Similarly the quadratic terms of the eccentricity vector components in can be ignored for almost circular orbits, i.e. can be approximated with
value given by is much smaller than the value given by and can be ignored. Similarly the quadratic terms of the eccentricity vector components in can be ignored for almost circular orbits, i.e. can be approximated with
-
Adding the contribution
contribution

to one gets-
This the difference equation saying that the eccentricity vector will describe a circle centered at the point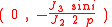 , the polar argument of the eccentricity vector increasing with
, the polar argument of the eccentricity vector increasing with 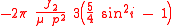 radians between consecutive orbits.
radians between consecutive orbits.
As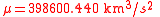
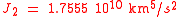
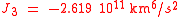
one gets for a polar orbit ( ) with
) with  that the center of the circle is
that the center of the circle is 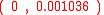 and the change of polar argument is 0.00400 radians per orbit.
and the change of polar argument is 0.00400 radians per orbit.
The latter figure means that the eccentricity vector will have described a full circle in 1569 orbits.
Selecting the initial mean eccentricity vector to the mean eccentricity vector will stay constant for successive orbits, i.e. the orbit is "frozen" because the secular perturbations of the
the mean eccentricity vector will stay constant for successive orbits, i.e. the orbit is "frozen" because the secular perturbations of the  term given by and of the
term given by and of the 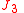 term given by cancel out.
term given by cancel out.
In terms of classical orbital elements this means that a "frozen" orbit should have the following (mean!) elements: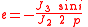

Modern theory
The modern theory of "Frozen orbits" is based on the algorithm given in.
For this the analytical expression is used to iteratively update the initial (mean) eccentricity vector to obtain that the (mean) eccentricity vector several orbits later computed by the precise numerical propagation takes precisely the same value. In this way the secular perturbation of the eccentricity vector caused by the term is used to counteract all secular perturbations, not only those (dominating) caused by the
term is used to counteract all secular perturbations, not only those (dominating) caused by the  term. One such additional secular perturbation that in this way can be compensated for is the one caused by the solar radiation pressure, this perturbation is discussed in the article "Orbital perturbation analysis (spacecraft)Orbital perturbation analysis (spacecraft)Isaac Newton in his Philosophiæ Naturalis Principia Mathematica demonstrated that the gravitational force between two mass points is inversely proportional to the square of the distance between the points and fully solved corresponding "two-body problem" demonstrating that radius vector between the...
term. One such additional secular perturbation that in this way can be compensated for is the one caused by the solar radiation pressure, this perturbation is discussed in the article "Orbital perturbation analysis (spacecraft)Orbital perturbation analysis (spacecraft)Isaac Newton in his Philosophiæ Naturalis Principia Mathematica demonstrated that the gravitational force between two mass points is inversely proportional to the square of the distance between the points and fully solved corresponding "two-body problem" demonstrating that radius vector between the...
".
Applying this algorithm for the case discussed above, i.e. a polar orbit ( ) with
) with  ignoring all other perturbing forces then the
ignoring all other perturbing forces then the  and the
and the 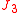 forces for the numerical propagation one gets exactly the same optimal average eccentricity vector as with the "classical theory", i.e.
forces for the numerical propagation one gets exactly the same optimal average eccentricity vector as with the "classical theory", i.e. 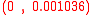 .
.
Including also the forces due to the higher zonal terms the optimal value changes to .
.
Assuming in addition a reasonable solar pressure (a "cross-sectional-area" of 0.05 square meters per kg, the direction to the Sun in the direction towards the ascending node) the optimal value for the average eccentricity vector gets what correponds to :
what correponds to : , i.e. the optimal value is no more
, i.e. the optimal value is no more 
This algorithm is implemented in the orbit control software used for the Earth observation satelliteEarth observation satelliteEarth observation satellites are satellites specifically designed to observe Earth from orbit, similar to reconnaissance satellites but intended for non-military uses such as environmental monitoring, meteorology, map making etc....
s ERS-1, ERS-2European Remote-Sensing SatelliteEuropean remote sensing satellite was the European Space Agency's first Earth-observing satellite. It was launched on July 17, 1991 into a Sun-synchronous polar orbit at a height of 782–785 km.-Instruments:...
and EnvisatEnvisatEnvisat is an Earth-observing satellite. It was launched on 1 March 2002 aboard an Ariane 5 from the Guyana Space Centre in Kourou, French Guyana into a Sun synchronous polar orbit at an altitude of...
Derivation of the closed form expressions for the J3 perturbation
The main perturbing force to be counter-acted to have a "frozen orbit" is the "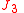 force", i.e. the gravitational force caused by an imperfect symmetry north/south of the Earth, and the "classical theory" is based on the closed form expression for this "
force", i.e. the gravitational force caused by an imperfect symmetry north/south of the Earth, and the "classical theory" is based on the closed form expression for this "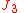 perturbation". With the "modern theory" this explicit closed form expression is not directly used but it is certainly still worthwhile to derive it.
perturbation". With the "modern theory" this explicit closed form expression is not directly used but it is certainly still worthwhile to derive it.
The derivation of this expression can be done as follows:
The potential from a zonal term is rotational symmetric around the polar axis of the Earth and corresponding force is entirely in a longitudial plane with one component in the radial direction and one component
in the radial direction and one component 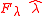 with the unit vector
with the unit vector 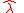 orthogonal to the radial direction towards north. These directions
orthogonal to the radial direction towards north. These directions  and
and 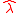 are illustrated in Figure 1.
are illustrated in Figure 1.
In the article Geopotential model it is shown that these force components caused by the term are
term are
-
To be able to apply relations derived in the article Orbital perturbation analysis (spacecraft)Orbital perturbation analysis (spacecraft)Isaac Newton in his Philosophiæ Naturalis Principia Mathematica demonstrated that the gravitational force between two mass points is inversely proportional to the square of the distance between the points and fully solved corresponding "two-body problem" demonstrating that radius vector between the...
the force component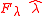 must be split into two orthogonal components
must be split into two orthogonal components  and
and  as illustrated in figure 2
as illustrated in figure 2
Let make up a rectangular coordinate system with origin in the center of the Earth (in the center of the Reference ellipsoidReference ellipsoidIn geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
make up a rectangular coordinate system with origin in the center of the Earth (in the center of the Reference ellipsoidReference ellipsoidIn geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
) such that points in the direction north and such that
points in the direction north and such that  are in the equatorial plane of the Earth with
are in the equatorial plane of the Earth with  pointing towards the ascending nodeOrbital nodeAn orbital node is one of the two points where an orbit crosses a plane of reference to which it is inclined. An orbit which is contained in the plane of reference has no nodes.-Planes of reference:...
pointing towards the ascending nodeOrbital nodeAn orbital node is one of the two points where an orbit crosses a plane of reference to which it is inclined. An orbit which is contained in the plane of reference has no nodes.-Planes of reference:...
, i.e. towards the blue point of Figure 2.
The components of the unit vectors
making up the local coordinate system (of which are illustrated in figure 2) relative the
are illustrated in figure 2) relative the  are
are
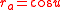



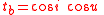




where is the polar argument of
is the polar argument of  relative the orthogonal unit vectors
relative the orthogonal unit vectors  and
and  in the orbital plane
in the orbital plane
Firstly

where is the angle between the equator plane and
is the angle between the equator plane and  (between the green points of figure 2) and from equation (12) of the article Geopotential model one therefore gets that
(between the green points of figure 2) and from equation (12) of the article Geopotential model one therefore gets that
-
Secondly the projection of direction north, , on the plane spanned by
, on the plane spanned by  is
is

and this projection is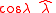
where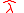 is the unit vector
is the unit vector 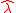 orthogonal to the radial direction towards north illustrated in figure 1.
orthogonal to the radial direction towards north illustrated in figure 1.
From equation one therefore gets that

and therefore:-
-
In the article Orbital perturbation analysis (spacecraft)Orbital perturbation analysis (spacecraft)Isaac Newton in his Philosophiæ Naturalis Principia Mathematica demonstrated that the gravitational force between two mass points is inversely proportional to the square of the distance between the points and fully solved corresponding "two-body problem" demonstrating that radius vector between the...
it is further shown that the secular perturbation of the orbital pole is
is
-
Introducing the expression for of in one gets
of in one gets
-
The fraction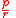 is
is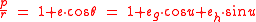
where


are the components of the eccentricity vector in the coordinate system.
coordinate system.
As all integrals of type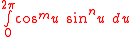
are zero if not both and
and  are even one has that
are even one has that
-
and
-
from what follows that
-
where
 and
and 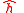 are the base vectors of the rectangular coordinate system in the plane of the reference Kepler orbit with
are the base vectors of the rectangular coordinate system in the plane of the reference Kepler orbit with 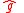 in the equatorial plane towards the ascending node and
in the equatorial plane towards the ascending node and  is the polar argument relative this equatorial coordinate system
is the polar argument relative this equatorial coordinate system
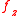 is the force component (per unit mass) in the direction of the orbit pole
is the force component (per unit mass) in the direction of the orbit pole 
In the article Orbital perturbation analysis (spacecraft)Orbital perturbation analysis (spacecraft)Isaac Newton in his Philosophiæ Naturalis Principia Mathematica demonstrated that the gravitational force between two mass points is inversely proportional to the square of the distance between the points and fully solved corresponding "two-body problem" demonstrating that radius vector between the...
it is shown that the secular perturbation of the eccentricity vector is
-
where
 is the usual local coordinate system with unit vector
is the usual local coordinate system with unit vector  directed away from the Earth
directed away from the Earth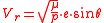 - the velocity component in direction
- the velocity component in direction 
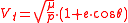 - the velocity component in direction
- the velocity component in direction 
Introducing the expression for of and in one gets
of and in one gets
-
Using that
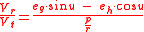
the integral above can be split in 8 terms:
-
As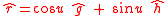

one gets using that

and that all integrals of type

are zero if not both and
and  are even:
are even:
Term 1
-
Term 2
-
Term 3
-
Term 4
-
Term 5
-
Term 6
-
Term 7
-
Term 8
-
As
-
It follows that
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-

