Orbital perturbation analysis (spacecraft)
Encyclopedia
Isaac Newton
in his Philosophiæ Naturalis Principia Mathematica demonstrated that the gravitational force between two mass points is inversely proportional to the square of the distance between the points and fully solved corresponding "two-body problem"
demonstrating that radius vector between the two points would describe an ellipse
. But already for the three body problem no exact closed form analytical form could be found. Instead approximate methods were developed, this is the method of "Orbital perturbation analysis". With this technique a quite accurate mathematical description of the trajectories of all the planets could be obtained. Especially critical was the mathematical modeling of the orbit of the Moon
as the deviations from a pure Kepler orbit
around the Earth due to the gravitational force of the Sun (i.e. one has indeed the three body problem) are much larger than deviations of the orbits of the planets from Sun-centered Kepler orbit
s caused by the gravitational attraction between the planets. With the availability of digital computers and the easiness to propagate orbits with numerical methods this problem partly disappeared, the motion of all celestial bodies including planets, satellites, asteroids and comets can be modeled and predicted with almost perfect accuracy using the method of the numerical propagation of the trajectories. Never-the-less several analytical closed form expressions for the effect of such additional "perturbing forces" are still very useful
follow in first approximation a Kepler orbit
around a central body. For a satellite (artificial or natural) this central body is a planet. But both due to gravitational forces caused by the Sun and other celestial bodies and due to the flattening of its planet (caused by its rotation which makes the planet slightly oblate and therefore the result of the Shell theorem
not fully applicable) the satellite will follow an orbit that deviates more from a pure Kepler orbit then what is the case for the planets.
The precise modeling of the motion of the Moon has because of this been a difficult task. The best and most accurate modeling for the Moon orbit before the availability of digital computers was obtained with the complicated Delunay
and Brown
's lunar theories
.
But the most important of these perturbation effects, the precession of the orbital plane caused by the slightly oblate shape of the Earth, was already fully understood by Isaac Newton
who estimated the oblateness of the Earth from the observed rate of precession of the orbital plane of the Moon.
For man-made spacecraft orbiting the Earth at comparatively low altitudes the deviations from a Kepler orbit are much larger than for the Moon. The approximation of the gravitational force of the Earth to be that of a homogeneous sphere gets worse the closer one gets to the Earth surface and the majority of the artificial Earth satellites are in orbits that are only a few hundred kilometers over the Earth surface. Further more they are (as opposed to the Moon) significantly affected by the solar radiation pressure because of their large cross-section to mass ratio, this applies in particular to 3-axis stabilized spacecraft with large solar arrays. In addition they are significantly affected by rarefied air unless above 800–1000 km (The air drag at high altitudes strongly depending on the solar activity!)
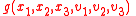
of the position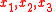
and the velocity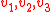
From the chain rule of differentiation one gets that the time derivative of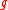
is
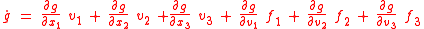
where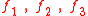
are the components of the force per unit mass acting on the body.
If now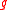
is a "constant of motion" for a Kepler orbit
like for example an orbital element and the force is corresponding "Kepler force"
one has that
.
If the force is the sum of the "Kepler force" and an additional force (force per unit mass)
i.e.
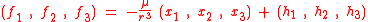
one therefore has
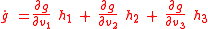
and that the change of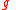
in the time from 
to 
is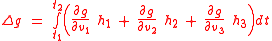
If now the additional force
is sufficiently small that the motion will be close to that of a Kepler orbit
one gets an approximate value for
by evaluating this integral assuming
to precisely follow this Kepler orbit
.
In general one wants to find an approximate expression for the change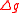
over one orbital revolution using the true anomaly 
as integration variable, i.e. as
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
in his Philosophiæ Naturalis Principia Mathematica demonstrated that the gravitational force between two mass points is inversely proportional to the square of the distance between the points and fully solved corresponding "two-body problem"
Kepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
demonstrating that radius vector between the two points would describe an ellipse
Kepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
. But already for the three body problem no exact closed form analytical form could be found. Instead approximate methods were developed, this is the method of "Orbital perturbation analysis". With this technique a quite accurate mathematical description of the trajectories of all the planets could be obtained. Especially critical was the mathematical modeling of the orbit of the Moon
Lunar theory
Lunar theory attempts to account for the motions of the Moon. There are many irregularities in the Moon's motion, and many attempts have been made over a long history to account for them. After centuries of being heavily problematic, the lunar motions are nowadays modelled to a very high degree...
as the deviations from a pure Kepler orbit
Kepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
around the Earth due to the gravitational force of the Sun (i.e. one has indeed the three body problem) are much larger than deviations of the orbits of the planets from Sun-centered Kepler orbit
Kepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
s caused by the gravitational attraction between the planets. With the availability of digital computers and the easiness to propagate orbits with numerical methods this problem partly disappeared, the motion of all celestial bodies including planets, satellites, asteroids and comets can be modeled and predicted with almost perfect accuracy using the method of the numerical propagation of the trajectories. Never-the-less several analytical closed form expressions for the effect of such additional "perturbing forces" are still very useful
Orbital perturbation of spacecraft orbits
All celestial bodies of the Solar SystemSolar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
follow in first approximation a Kepler orbit
Kepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
around a central body. For a satellite (artificial or natural) this central body is a planet. But both due to gravitational forces caused by the Sun and other celestial bodies and due to the flattening of its planet (caused by its rotation which makes the planet slightly oblate and therefore the result of the Shell theorem
Shell theorem
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body...
not fully applicable) the satellite will follow an orbit that deviates more from a pure Kepler orbit then what is the case for the planets.
The precise modeling of the motion of the Moon has because of this been a difficult task. The best and most accurate modeling for the Moon orbit before the availability of digital computers was obtained with the complicated Delunay
Charles-Eugène Delaunay
Charles-Eugène Delaunay was a French astronomer and mathematician. His lunar motion studies were important in advancing both the theory of planetary motion and mathematics.-Life:...
and Brown
Ernest William Brown
Ernest William Brown FRS was a British mathematician and astronomer, who spent the majority of his career working in the United States....
's lunar theories
Lunar theory
Lunar theory attempts to account for the motions of the Moon. There are many irregularities in the Moon's motion, and many attempts have been made over a long history to account for them. After centuries of being heavily problematic, the lunar motions are nowadays modelled to a very high degree...
.
But the most important of these perturbation effects, the precession of the orbital plane caused by the slightly oblate shape of the Earth, was already fully understood by Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
who estimated the oblateness of the Earth from the observed rate of precession of the orbital plane of the Moon.
For man-made spacecraft orbiting the Earth at comparatively low altitudes the deviations from a Kepler orbit are much larger than for the Moon. The approximation of the gravitational force of the Earth to be that of a homogeneous sphere gets worse the closer one gets to the Earth surface and the majority of the artificial Earth satellites are in orbits that are only a few hundred kilometers over the Earth surface. Further more they are (as opposed to the Moon) significantly affected by the solar radiation pressure because of their large cross-section to mass ratio, this applies in particular to 3-axis stabilized spacecraft with large solar arrays. In addition they are significantly affected by rarefied air unless above 800–1000 km (The air drag at high altitudes strongly depending on the solar activity!)
Mathematical approach
Consider any function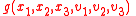of the position
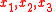
and the velocity
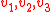
From the chain rule of differentiation one gets that the time derivative of
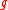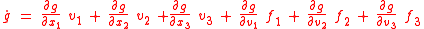
iswhere
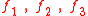are the components of the force per unit mass acting on the body.If now
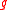is a "constant of motion" for a Kepler orbitKepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
like for example an orbital element and the force is corresponding "Kepler force"
one has that
.If the force is the sum of the "Kepler force" and an additional force (force per unit mass)
i.e.
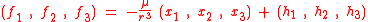
one therefore has
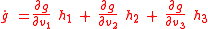
and that the change of
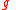in the time from to is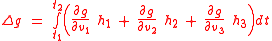If now the additional force
is sufficiently small that the motion will be close to that of a Kepler orbitKepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
one gets an approximate value for
by evaluating this integral assuming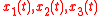 to precisely follow this Kepler orbitKepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
.
In general one wants to find an approximate expression for the change
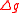over one orbital revolution using the true anomaly as integration variable, i.e. as
-
This integral is evaluated setting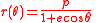
, the elliptical Kepler orbit in polar angles.
For the transformation of integration variable from time to true anomalyTrue anomalyIn celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
it was used that the angular momentum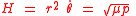
by definition of the parameter 
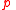for a Kepler orbit (see equation (13) of the Kepler orbitKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
article).
For the very important case that the Kepler orbit is circular or almost circular
and takes the simpler form
-
where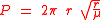
is the orbital period
Perturbation of the semi-major axis/orbital period
For an elliptic Kepler orbitKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
the sum of the kinetic and the potential energy
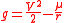
where
is the orbital velocity
is a constant and equal to
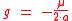(Equation (44) of the Kepler orbitKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
article)
If
is the perturbing force and 
is the velocity vector of the Kepler orbit the equation takes the form:
-
and for a circular or almost circular orbit
-
From the change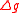
of the parameter 
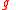the new semi-major axis 
and the new period 
are computed (relations (43) and (44) of the Kepler orbitKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
article).
Perturbation of the orbital plane
Let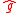
and 
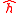make up a rectangular coordinate system in the plane of the reference Kepler orbit. If 
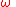is the argument of perigee relative the 
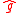and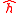 
coordinate system the true anomaly 
is given by 
and the approximate change 
of the orbital pole 
(defined as the unit vector in the direction of the angular momentum) is
-
where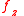
is the component of the perturbing force in the 
direction,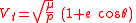 
is the velocity component of the Kepler orbit orthogonal to radius vector and 
is the distance to the center of the Earth.
For a circular or almost circular orbit simplifies to
-
Example
In a circular orbit a low-force propulsion system (Ion thrusterIon thrusterAn ion thruster is a form of electric propulsion used for spacecraft propulsion that creates thrust by accelerating ions. Ion thrusters are categorized by how they accelerate the ions, using either electrostatic or electromagnetic force. Electrostatic ion thrusters use the Coulomb force and...
) generates a thrust (force per unit mass) of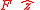
in the direction of the orbital pole in the half of the orbit for which 
is positive and in the opposite direction in the other half. The resulting change of orbit pole after one orbital revolution of duration 
is
-
The average change rate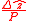
is therefore
-
where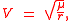
is the orbital velocity in the circular Kepler orbit.
Perturbation of the eccentricity vector
Rather than applying (1) and (2) on the partial derivatives of the orbital elements eccentricity and argument of perigee directly one should apply these relations for the eccentricity vectorEccentricity vectorIn astrodynamics, the eccentricity vector of a Kepler orbit is the vector pointing towards the periapsis having a magnitude equal to the orbit's scalar eccentricity. The magnitude is unitless. For Kepler orbits the eccentricity vector is a constant of motion...
. First of all the typical application is a near-circular orbit. But there are also mathematical advantages working with the partial derivatives of the components of this vector also for orbits with a significant eccentricity.
Equations (60), (55) and (52) of the Kepler orbitKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
article say that the eccentricity vector is
where
from which follows that
where
(Equations (18) and (19) of the Kepler orbitKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
article)
The eccentricity vector is by definition always in the osculatingOsculating orbitIn astronomy, and in particular in astrodynamics, the osculating orbit of an object in space is the gravitational Kepler orbit In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space (at a given moment of time) is the gravitational Kepler orbit In astronomy,...
orbital plane spanned by
and 
and formally there is also a derivative
with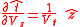
corresponding to the rotation of the orbital plane
But in practice the in-plane change of the eccentricity vector is computed as
-
ignoring the out-of-plane force and the new eccentricity vector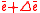
is subsequently projected to the new orbital plane orthogonal to the new orbit normal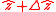
computed as described above.
Example
The Sun is in the orbital plane of a spacecraft in a circular orbit with radius
and consequently with a constant orbital velocity 
. If 
and 
make up a rectangular coordinate system in the orbital plane such that 
points to the Sun and assuming that the solar radiation pressure force per unit mass 
is constant one gets that
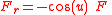
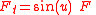
where
is the polar angle of 
in the 
, 
system. Applying one gets that
-
This means the eccentricity vector will gradually increase in the direction
orthogonal to the Sun direction. This is true for any orbit with a small eccentricity, the direction of the small eccentricity vector does not matter. As 
is the orbital period this means that the average rate of this increase will be
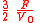
The effect of the Earth flattening
In the article Geopotential model the modeling of the gravitational field as a sum of spherical harmonics is discussed. The by far dominating term is the "J2-term". This is a "zonal term" and corresponding force is therefore completely in a longitudinal plane with one component
in the radial direction and one component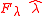 
with the unit vector 
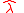orthogonal to the radial direction towards north. These directions 
and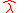 
are illustrated in Figure 1.
To be able to apply relations derived in the previous section the force component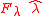
must be split into two orthogonal components 
and 
as illustrated in figure 2
Let
make up a rectangular coordinate system with origin in the center of the Earth (in the center of the Reference ellipsoidReference ellipsoidIn geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
) such that
points in the direction north and such that 
are in the equatorial plane of the Earth with 
pointing towards the ascending nodeOrbital nodeAn orbital node is one of the two points where an orbit crosses a plane of reference to which it is inclined. An orbit which is contained in the plane of reference has no nodes.-Planes of reference:...
, i.e. towards the blue point of Figure 2.
The components of the unit vectors
making up the local coordinate system (of which
are illustrated in figure 2) relative the 
are
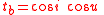
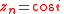
where
is the polar argument of 
relative the orthogonal unit vectors 
and 
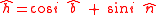in the orbital plane
Firstly
where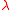
is the angle between the equator plane and 
(between the green points of figure 2) and from equation (12) of the article Geopotential model one therefore gets that
-
Secondly the projection of direction north,
, on the plane spanned by 
is
and this projection is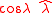
where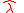
is the unit vector 
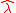orthogonal to the radial direction towards north illustrated in figure 1.
From equation (12) of the article Geopotential model one therefore gets that
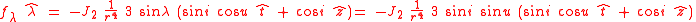
and therefore:-
-
Perturbation of the orbital plane
From and one gets that
-
The fraction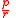
is
where
is the eccentricity
and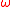
is the argument of perigee
of the reference Kepler orbitKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
As all integrals of type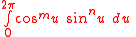
are zero if not both
and 
are even one gets from that
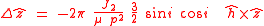
As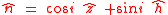
this can be written-
As
is an inertially fixed vector (the direction of the spin axis of the Earth) relation is the equation of motion for a unit vector 
describing a cone around 
with a precession rate (radians per orbit) of 
In terms of orbital elements this is expressed as
-
-
where
is the inclination of the orbit to the equatorial plane of the Earth
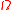is the right ascension of the ascending node
Perturbation of the eccentricity vector
From , and follows that in-plane perturbation of the eccentricity vector is
-
the new eccentricity vector being the projection of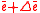
on the new orbital plane orthogonal to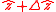
where
is given by
Relative the coordinate system
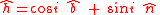
one has that
Using that
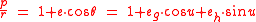
and that
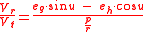
where
are the components of the eccentricity vector in the
coordinate system this integral can be evaluated analytically, the result is
-
This the difference equation of motion for the eccentricity vector
to form a circle, the magnitude of the eccentricity 
staying constant.
Translating this to orbital elements it must be remembered that the new eccentricity vector obtained by adding
to the old 
must be projected to the new orbital plane obtained by applying and
This is illustrated in figure 3:
To the change in argument of the eccentricity vector
must be added an increment due to the precession of the orbital plane (caused by the out-of-plane force component) amounting to
One therefore gets that
-
-
In terms of the components of the eccentricity vector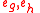
relative the coordinate system 
that precesses around the polar axis of the Earth the same is expressed as follows
-
where the first term is the in-plane perturbation of the eccentricity vector and the second is the effect of the new position of the ascending node in the new plane
From follows that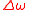
is zero if 
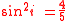. This fact is used for Molniya orbitMolniya orbitMolniya orbit is a type of highly elliptical orbit with an inclination of 63.4 degrees, an argument of perigee of -90 degree and an orbital period of one half of a sidereal day...
s having an inclination of 63.4 deg. An orbit with an inclination of 180 - 63.4 deg = 116.6 deg would in the same way have a constant argument of perigee.
Proof
Proof that the integral
-
where: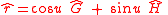
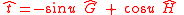
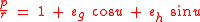
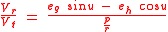
has the value-
Integrating the first term of the integrand one gets:
-
and
-
For the second term one gets:
-
and
-
For the third term one gets:-
and
-
For the fourth term one gets:
-
and
-
Adding the right hand sides of , , and one gets
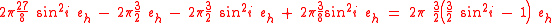
Adding the right hand sides of , , and one gets
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
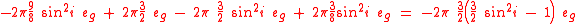