
Full and faithful functors
Encyclopedia
In category theory
, a faithful functor (resp. a full functor) is a functor
which is injective (resp. surjective) when restricted to each set of morphism
s that have a given source and target.
Explicitly, let C and D be (locally small) categories
and let F : C → D be a functor from C to D. The functor F induces a function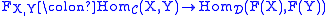
for every pair of objects X and Y in C. The functor F is said to be
for each X and Y in C.
A faithful functor need not be injective on objects or morphisms. That is, two objects X and X′ may map to the same object in D (which is why the range of a full and faithful functor is not necessarily isomorphic to C), and two morphisms f : X → Y and f′ : X′ → Y′ (with different domains/codomains) may map to the same morphism in D. Likewise, a full functor need not be surjective on objects or morphisms. There may be objects in D not of the form FX for some X in C. Morphisms between such objects clearly cannot come from morphisms in C.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a faithful functor (resp. a full functor) is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
which is injective (resp. surjective) when restricted to each set of morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s that have a given source and target.
Explicitly, let C and D be (locally small) categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
and let F : C → D be a functor from C to D. The functor F induces a function
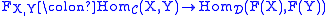
for every pair of objects X and Y in C. The functor F is said to be
- faithful if FX,Y is injective
- full if FX,Y is surjective
- fully faithful if FX,Y is bijective
for each X and Y in C.
A faithful functor need not be injective on objects or morphisms. That is, two objects X and X′ may map to the same object in D (which is why the range of a full and faithful functor is not necessarily isomorphic to C), and two morphisms f : X → Y and f′ : X′ → Y′ (with different domains/codomains) may map to the same morphism in D. Likewise, a full functor need not be surjective on objects or morphisms. There may be objects in D not of the form FX for some X in C. Morphisms between such objects clearly cannot come from morphisms in C.
Examples
- The forgetful functorForgetful functorIn mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
U : Grp → Set is faithful as each group maps to a unique set and the group homomorphism are a subset of the functions. This functor is not full as there are functions between groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s which are not group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s. A category with a faithful functor to Set is (by definition) a concrete categoryConcrete categoryIn mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
; in general, that forgetful functor is not full.
- Let F : Set → Set be the functor which maps every set to the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
and every function to the empty functionEmpty functionIn mathematics, an empty function is a function whose domain is the empty set. For each set A, there is exactly one such empty functionf_A: \varnothing \rightarrow A....
. Then F is full, but is neither injective on objects nor on morphisms.
- The inclusion functor Ab → Grp is fully faithful.

