Full reptend prime
Encyclopedia
In number theory
, a full reptend prime or long prime in base
b is a prime number
p such that the formula
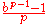
(where p does not divide
b) gives a cyclic number
. Therefore the digital expansion of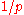
in base b repeats the digits of the corresponding cyclic number infinitely. Base 10
may be assumed if no base is specified.
The first few values of p for which this formula produces cyclic numbers in decimal are
For example, the case b = 10, p = 7 gives the cyclic number 142857
, thus, 7 is a full reptend prime. Furthermore, 1 divided by 7 written out in base 10 is 0.142857142857142857142857...
Not all values of p will yield a cyclic number using this formula; for example p = 13 gives 076923076923. These failed cases will always contain a repetition of digits (possibly several).
The known pattern to this sequence comes from algebraic number theory
, specifically, this sequence is the set of primes p such that 10 is a primitive root modulo p
. Artin's conjecture on primitive roots
is that this sequence contains 37.395..% of the primes.
The term "long prime" was used by John Conway
and Richard Guy in their Book of Numbers. Confusingly, Sloane's OEIS refers to these primes as "cyclic numbers."
The corresponding cyclic number to prime p will possess p - 1 digits if and only if
p is a full reptend prime.
can show that any prime of the following forms:
can never be a full reptend prime in base-10. The first primes of these forms, with their periods, are:
However, studies show that two-thirds of primes of the form 40k+n, where n ≠ {1,3,9,13,27,31,37,39} are full reptend primes. For some sequences, the preponderance of full reptend primes is much greater. For instance, 285 of the 295 primes of form 120k+23 below 100000 are full reptend primes, with 20903 being the first that is not full reptend.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a full reptend prime or long prime in base
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
b is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p such that the formula
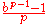
(where p does not divide
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
b) gives a cyclic number
Cyclic number
A cyclic number is an integer in which cyclic permutations of the digits are successive multiples of the number. The most widely known is 142857:For example:Multiples of these fractions exhibit cyclic permutation:...
. Therefore the digital expansion of
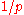in base b repeats the digits of the corresponding cyclic number infinitely. Base 10Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
may be assumed if no base is specified.
The first few values of p for which this formula produces cyclic numbers in decimal are
- 7, 1717 (number)17 is the natural number following 16 and preceding 18. It is prime.In spoken English, the numbers 17 and 70 are sometimes confused because they sound similar. When carefully enunciated, they differ in which syllable is stressed: 17 vs 70...
, 1919 (number)19 is the natural number following 18 and preceding 20. It is a prime number.In English speech, the numbers 19 and 90 are often confused. When carefully enunciated, they differ in which syllable is stressed: 19 vs 90...
, 2323 (number)23 is the natural number following 22 and preceding 24.- In mathematics :Twenty-three is the ninth prime number, the smallest odd prime that is not a twin prime. Twenty-three is also the fifth factorial prime, the third Woodall prime...
, 2929 (number)29 is the natural number following 28 and preceding 30.-In mathematics:It is the tenth prime number, and also the fourth primorial prime. It forms a twin prime pair with thirty-one, which is also a primorial prime. Twenty-nine is also the sixth Sophie Germain prime. It is also the sum of three...
, 4747 (number)47 is the natural number following 46 and preceding 48.-In mathematics:Forty-seven is the fifteenth prime number, a safe prime, the thirteenth supersingular prime, and the sixth Lucas prime. Forty-seven is a highly cototient number...
, 5959 (number)59 is the natural number following 58 and preceding 60.-In mathematics:Fifty-nine is the 17th smallest prime number. The next is sixty-one, with which it comprises a twin prime. 59 is an irregular prime, a safe prime and the 14th supersingular prime. It is an Eisenstein prime with no imaginary...
, 6161 (number)61 is the natural number following 60 and preceding 62.-In mathematics:It is the 18th prime number. The previous is 59, with which it comprises a twin prime. Sixty-one is a cuban prime of the form p = / , x = y + 1....
, 9797 (number)97 is the natural number following 96 and preceding 98.-In mathematics:97 is the 25th prime number , following 89 and preceding 101. 97 is a Proth prime as it is 3 × 25 + 1.The numbers 97, 907, 9007, 90007 and 900007 are happy primes...
, 109109 (number)109 is the natural number following 108 and preceding 110.-In mathematics:One hundred [and] nine is the 29th prime number, and also a Chen prime. The previous prime is 107, making them both twin primes...
, 113113 (number)113 is the natural number following 112 and preceding 114.-In mathematics:One hundred [and] thirteen is the 30th prime number, following 109 and preceding 127, a Sophie Germain prime, a Chen prime and a Proth prime as it is a prime number of the form 7 × 24 + 1...
, 131131 (number)131 is the natural number following 130 and preceding 132.-In mathematics:131 is a Sophie Germain prime, the second 3-digit palindromic prime, and also a permutable prime with 113 and 311. It can be expressed as the sum of three consecutive primes, 131 = 41 + 43 + 47. 131 is an Eisenstein prime...
, 149149 (number)149 is the natural number between 148 and 150. It is also a prime number.-In mathematics:*149 is the 35th prime number, and with the next prime number, 151, is a twin prime, thus 149 is a Chen prime. 149 is a strong prime in the sense that it is more than the arithmetic mean of its two neighboring...
, 167167 (number)167 is the natural number following 166 and preceding 168.-In mathematics:* 167 is an odd number* 167 is a Chen prime, since the next odd number, 169, is a square of a prime...
, 179179 (number)179 is the natural number following 178 and preceding 180.-In mathematics:* 179 is an odd number* 179 is a deficient number, as 1 is less than 179* 179 is a Gaussian number* 179 is an odious number* 179 is a square-free number...
, 181181 (number)181 is the natural number between 180 and 182.-In mathematics:* 181 is an odd number* 181 is a centered number** 181 is a centered pentagonal number** 181 is a centered 12-gonal number** 181 is a centered 18-gonal number...
, 193193 (number)193 is the natural number following 192 and preceding 194.-In mathematics:* 193 is an odd number* 193 is a centered 32-gonal number* 193 is a deficient number, as 1 is less than 193* 193 is a happy number* 193 is a lucky number...
, 223223 (number)223 is the natural number between 222 and 224. It is also a prime number.-In mathematics:223 is a long prime, a strong prime, a lucky prime and a sexy prime .223 is the fourth Carol number and the third to be prime....
, 229229 (number)229 is the natural number between 228 and 230. It is also a prime number.The North American telephone area code 229 is assigned to the area around the city of Albany in southwestern Georgia in North America....
, 233233 (number)233 is the natural number between 232 and 234. It is also a prime number.-In mathematics:233 is an irregular prime, a full reptend prime, a cousin prime, a Chen prime, a Fibonacci prime and a sexy prime. It is the 13th Fibonacci number. It is an Eisenstein prime of the form 3n - 1 with no...
, 257, 263263 (number)263 is the natural number between 262 and 264. It is also a prime number.-In mathematics:263 is an irregular prime, an Eisenstein prime, a long prime, a Chen prime, a Gaussian prime, a happy prime, a sexy prime, a safe prime, and a Higgs prime....
, 269269 (number)269 is the natural number between 268 and 270. It is also a prime number.-In mathematics:269 is a regular prime, an Eisenstein prime with no imaginary part, a long prime, a Chen prime, a Pillai prime, a Pythagorean prime, a twin prime, a sexy prime, a Higgs prime, a strong prime, and a highly...
, 313313 (number)313 is an integer following 312 and preceding 314. 313 is a:* prime number* twin prime with 311* centered square number* long prime* pythagorean prime* regular prime* palindromic prime in both decimal and binary.* truncatable prime* happy number...
, 337, 367, 379, 383, 389, 419, 433, 461, 487, 491, 499, 503, 509, 541, 571, 577, 593, 619, 647, 659, 701, 709, 727, 743, 811, 821, 823, 857, 863, 887, 937, 941, 953, 971, 977, 983 …
For example, the case b = 10, p = 7 gives the cyclic number 142857
142857 (number)
142857 is the six repeating digits of 1/7, 0., and is the best-known cyclic number in base 10. If it is multiplied by 2, 3, 4, 5, or 6, the answer will be a cyclic permutation of itself, and will correspond to the repeating digits of 2/7, 3/7, 4/7, 5/7, or 6/7, respectively.- Calculations :- 22/7...
, thus, 7 is a full reptend prime. Furthermore, 1 divided by 7 written out in base 10 is 0.142857142857142857142857...
Not all values of p will yield a cyclic number using this formula; for example p = 13 gives 076923076923. These failed cases will always contain a repetition of digits (possibly several).
The known pattern to this sequence comes from algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, specifically, this sequence is the set of primes p such that 10 is a primitive root modulo p
Primitive root modulo n
In modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
. Artin's conjecture on primitive roots
Artin's conjecture on primitive roots
In number theory, Artin's conjecture on primitive roots states that a given integer a which is not a perfect square and not −1 is a primitive root modulo infinitely many primes p. The conjecture also ascribes an asymptotic density to these primes...
is that this sequence contains 37.395..% of the primes.
The term "long prime" was used by John Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
and Richard Guy in their Book of Numbers. Confusingly, Sloane's OEIS refers to these primes as "cyclic numbers."
The corresponding cyclic number to prime p will possess p - 1 digits if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
p is a full reptend prime.
Patterns of occurrence of full reptend primes
Advanced modular arithmeticModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
can show that any prime of the following forms:
can never be a full reptend prime in base-10. The first primes of these forms, with their periods, are:
| 40k+1 | 40k+3 | 40k+9 | 40k+13 | 40k+27 | 40k+31 | 40k+37 | 40k+39 |
|---|---|---|---|---|---|---|---|
| 41 period 5 |
43 period 21 |
89 period 44 |
13 period 6 |
67 period 33 |
31 period 15 |
37 period 3 |
79 period 13 |
| 241 period 30 |
83 period 41 |
409 period 204 |
53 period 13 |
107 period 53 |
71 period 35 |
157 period 78 |
199 period 99 |
| 281 period 28 |
163 period 81 |
449 period 32 |
173 period 43 |
227 period 113 |
151 period 75 |
197 period 98 |
239 period 7 |
| 401 period 200 |
283 period 141 |
569 period 284 |
293 period 146 |
307 period 153 |
191 period 95 |
277 period 69 |
359 period 179 |
However, studies show that two-thirds of primes of the form 40k+n, where n ≠ {1,3,9,13,27,31,37,39} are full reptend primes. For some sequences, the preponderance of full reptend primes is much greater. For instance, 285 of the 295 primes of form 120k+23 below 100000 are full reptend primes, with 20903 being the first that is not full reptend.