Fundamental theorem on homomorphisms
Encyclopedia
In abstract algebra
, the fundamental theorem
on homomorphisms, also known as the fundamental homomorphism theorem, relates the structure of two objects between which a homomorphism
is given, and of the kernel
and image of the homomorphism.
The homomorphism theorem is used to prove the isomorphism theorem
s.
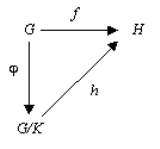
s G and H and a group homomorphism
f : G→H, let K be a normal subgroup
in G and φ the natural surjective homomorphism G→G/K. If K ⊂ ker
(f) then there exists a unique homomorphism h:G/K→H such that f = h φ.
The situation is described by the following commutative diagram
:
By setting K = ker(f) we immediately get the first isomorphism theorem.
s, vector space
s, modules
, and rings
.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the fundamental theorem
Fundamental theorem
The fundamental theorem of a field of mathematics is the theorem considered central to that field. The naming of such a theorem is not necessarily based on how often it is used or the difficulty of its proofs....
on homomorphisms, also known as the fundamental homomorphism theorem, relates the structure of two objects between which a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
is given, and of the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
and image of the homomorphism.
The homomorphism theorem is used to prove the isomorphism theorem
Isomorphism theorem
In mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
s.
Group theoretic version
Given two groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s G and H and a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
f : G→H, let K be a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
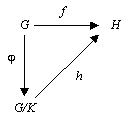
in G and φ the natural surjective homomorphism G→G/K. If K ⊂ ker
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
(f) then there exists a unique homomorphism h:G/K→H such that f = h φ.
The situation is described by the following commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:

By setting K = ker(f) we immediately get the first isomorphism theorem.
Other versions
Similar theorems are valid for monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s, vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, and rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.

