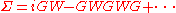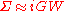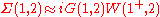GW approximation
Encyclopedia
The GW approximation is an approximation made in order to calculate the self-energy
of a many-body system of electrons. The approximation is that the expansion of the self-energy Σ in terms of the single particle Green function
G and the screened Coulomb interaction W (in units of )
)
can be truncated after the first term:
Another way to say the same thing is that that self-energy is expanded in a formal Taylor series in powers of the screened interaction W and the lowest order term is kept in the expansion in GWA.
The above formulae are schematic in nature and show the overall idea of the approximation. More precisely, if we label an electron coordinate with its position, spin, and time and bundle all three into a composite index (the numbers 1, 2, etc.), we have
where the "+" superscript means the time index is shifted forward by an infinitesimal amount. The GWA is then
To put this in context, if one replaces W by the bare Coulomb interaction (i.e. the usual 1/r interaction), one generates the standard perturbative series for the self-energy found in most many-body textbooks. The GWA with W replaced by the bare Coulomb yields nothing other than the Hartree-Fock
exchange potential (self-energy). Therefore, loosely speaking, the GWA represents a type of dynamically screened Hartree-Fock self-energy.
In a solid state system, the series for the self-energy in terms of W should converge much faster than the traditional series in the bare Coulomb interaction. This is because the screening of the medium reduces the effective strength of the Coulomb interaction: for example, if one places an electron at some position in a material and asks what the potential is at some other position in the material, the value is smaller than given by the bare Coulomb interaction (inverse distance between the points) because the other electrons in the medium polarize (move or distort their electronic states) so as to screen the electric field. Therefore, W is a smaller quantity than the bare Coulomb interaction so that a series in W should have higher hopes of converging quickly.
To see the more rapid convergence, we can consider the simplest example involving the homogeneous or uniform electron gas which is characterized by an electron density or equivalently the average electron-electron separation or Wigner-Seitz radius
 . (We only present a scaling argument and will not compute numerical prefactors that are order unity.) Here are the key steps:
. (We only present a scaling argument and will not compute numerical prefactors that are order unity.) Here are the key steps:
where is the screening wave number that scales as
is the screening wave number that scales as 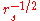
Thus for the bare Coulomb interaction, the ratio of Coulomb to kinetic energy is of order which is of order 2-5 for a typical metal and not small at all: in other words, the bare Coulomb interaction is rather strong and makes for a poor perturbative expansion. On the other hand, the ratio of a typical
which is of order 2-5 for a typical metal and not small at all: in other words, the bare Coulomb interaction is rather strong and makes for a poor perturbative expansion. On the other hand, the ratio of a typical  to the kinetic energy is greatly reduced by the screening and is of order
to the kinetic energy is greatly reduced by the screening and is of order  which is well behaved and smaller than unity even for large
which is well behaved and smaller than unity even for large  : the screened
: the screened
interaction is much weaker and is more likely to give a rapidly converging perturbative series.
Self-energy
In theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
of a many-body system of electrons. The approximation is that the expansion of the self-energy Σ in terms of the single particle Green function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
G and the screened Coulomb interaction W (in units of
 )
)
can be truncated after the first term:
Another way to say the same thing is that that self-energy is expanded in a formal Taylor series in powers of the screened interaction W and the lowest order term is kept in the expansion in GWA.
The above formulae are schematic in nature and show the overall idea of the approximation. More precisely, if we label an electron coordinate with its position, spin, and time and bundle all three into a composite index (the numbers 1, 2, etc.), we have
where the "+" superscript means the time index is shifted forward by an infinitesimal amount. The GWA is then
To put this in context, if one replaces W by the bare Coulomb interaction (i.e. the usual 1/r interaction), one generates the standard perturbative series for the self-energy found in most many-body textbooks. The GWA with W replaced by the bare Coulomb yields nothing other than the Hartree-Fock
Hartree-Fock
In computational physics and chemistry, the Hartree–Fock method is an approximate method for the determination of the ground-state wave function and ground-state energy of a quantum many-body system....
exchange potential (self-energy). Therefore, loosely speaking, the GWA represents a type of dynamically screened Hartree-Fock self-energy.
In a solid state system, the series for the self-energy in terms of W should converge much faster than the traditional series in the bare Coulomb interaction. This is because the screening of the medium reduces the effective strength of the Coulomb interaction: for example, if one places an electron at some position in a material and asks what the potential is at some other position in the material, the value is smaller than given by the bare Coulomb interaction (inverse distance between the points) because the other electrons in the medium polarize (move or distort their electronic states) so as to screen the electric field. Therefore, W is a smaller quantity than the bare Coulomb interaction so that a series in W should have higher hopes of converging quickly.
To see the more rapid convergence, we can consider the simplest example involving the homogeneous or uniform electron gas which is characterized by an electron density or equivalently the average electron-electron separation or Wigner-Seitz radius
Wigner-Seitz radius
The Wigner–Seitz radius r_s, named after Eugene Wigner and Frederick Seitz, is a parameter used frequently in condensed matter physics to describe the density of a system...
 . (We only present a scaling argument and will not compute numerical prefactors that are order unity.) Here are the key steps:
. (We only present a scaling argument and will not compute numerical prefactors that are order unity.) Here are the key steps:
- The kinetic energy of an electron scales as
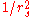
- The average electron-electron repulsion from the bare (unscreenedElectric field screeningScreening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases and conduction electrons in semiconductors and metals....
) Coulomb interaction scales as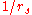 (simply the inverse of the typical separation)
(simply the inverse of the typical separation) - The electron gas dielectric function in the simplest Thomas-Fermi screening modelThomas-Fermi screeningThe mobile charge carriers damp down the electric fields in materials. This is called Electric field screening.Thomas-Fermi screening is one of many approximation methods for describing the screening....
for a wave vector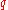 is
is
where
 is the screening wave number that scales as
is the screening wave number that scales as 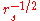
- Typical wave vectors
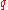 scale as
scale as 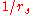 (again typical inverse separation)
(again typical inverse separation) - Hence a typical screening value is
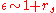
- The screened Coulomb interaction is

Thus for the bare Coulomb interaction, the ratio of Coulomb to kinetic energy is of order
 which is of order 2-5 for a typical metal and not small at all: in other words, the bare Coulomb interaction is rather strong and makes for a poor perturbative expansion. On the other hand, the ratio of a typical
which is of order 2-5 for a typical metal and not small at all: in other words, the bare Coulomb interaction is rather strong and makes for a poor perturbative expansion. On the other hand, the ratio of a typical  to the kinetic energy is greatly reduced by the screening and is of order
to the kinetic energy is greatly reduced by the screening and is of order  which is well behaved and smaller than unity even for large
which is well behaved and smaller than unity even for large  : the screened
: the screenedinteraction is much weaker and is more likely to give a rapidly converging perturbative series.
Software implementing the GW approximation
- BerkeleyGW - plane-wave pseudopotential method
- ABINITABINITABINIT is an open-source suite of programs for materials science, distributed under the GNU General Public License. ABINIT implements density functional theory, using a plane wave basis set and pseudopotentials, to compute the electronic density and derived properties of materials ranging from...
- plane-wave pseudopotential method - Spex - full-potential (linearized) augmented plane-wave (FP-LAPW) method
- SaX - plane-wave pseudopotential method
- YAMBO codeYAMBO codeYambo is an open source Many-body theory software package for study solids and molecular systems. It calculates the excited state properties of physical systems from first principles Yambo is an open source Many-body theory software package for study solids and molecular systems. It...
- plane-wave pseudopotential method - VASPVienna Ab-initio Simulation PackageThe Vienna Ab-initio Simulation Package, better known as VASP, is a package for performing ab initio quantum mechanical molecular dynamics using either Vanderbilt pseudopotentials, or the Projector Augmented Wave Method, and a plane wave basis set...
- projector-augmented-wave (PAW) method - GWW / Quantum ESPRESSO - Wannier-function pseudopotential method