Gabor transform
Encyclopedia
The Gabor transform, named after Dennis Gabor
, is a special case of the short-time Fourier transform
. It is used to determine the sinusoidal frequency
and phase
content of local sections of a signal as it changes over time. The function to be transformed is first multiplied by a Gaussian function, which can be regarded as a window, and the resulting function is then transformed with a Fourier transform to derive the time-frequency analysis
. The window function means that the signal near the time being analyzed will have higher weight. The Gabor transform of a signal x(t) is defined by this formula:
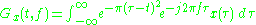
The Gaussian function has infinite range and it is impractical for implementation. But take a look at the distribution of Gaussian function.
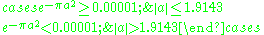
Gaussian function with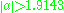
can be regarded as 0 and also can be ignored. Thus the Gabor transform can be simplified as
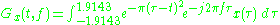
This simplification makes the Gabor transform practical and realizable.
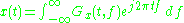
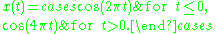
But if the total bandwidth available is 5Hz, other frequency bands except x(t) are wasted. Through time frequency analysis by applying the Gabor transform, the available bandwidth can be known and those frequency bands can be used for other applications and bandwidth is saved. The right side picture show the input signal x(t) and the output of the Gabor transform. As our expectation, the frequency distribution can be separate as two parts. One is t ≤ 0 and the other is t > 0. The white part is the frequency band occupied by x(t) and the black part is not used.
Dennis Gabor
Dennis Gabor CBE, FRS was a Hungarian-British electrical engineer and inventor, most notable for inventing holography, for which he later received the 1971 Nobel Prize in Physics....
, is a special case of the short-time Fourier transform
Short-time Fourier transform
The short-time Fourier transform , or alternatively short-term Fourier transform, is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time....
. It is used to determine the sinusoidal frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
and phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
content of local sections of a signal as it changes over time. The function to be transformed is first multiplied by a Gaussian function, which can be regarded as a window, and the resulting function is then transformed with a Fourier transform to derive the time-frequency analysis
Time-frequency analysis
In signal processing, time–frequency analysis comprises those techniques that study a signal in both the time and frequency domains simultaneously, using various time–frequency representations...
. The window function means that the signal near the time being analyzed will have higher weight. The Gabor transform of a signal x(t) is defined by this formula:
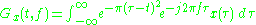
The Gaussian function has infinite range and it is impractical for implementation. But take a look at the distribution of Gaussian function.
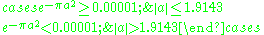
Gaussian function with
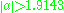can be regarded as 0 and also can be ignored. Thus the Gabor transform can be simplified as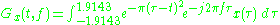This simplification makes the Gabor transform practical and realizable.
Inverse Gabor transform
The Gabor transform is invertible. The original signal can be recovered by the following equation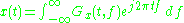Properties of the Gabor transform
The Gabor transform has many properties like those of the Fourier transform. These properties are listed in the following tables.| Signal | Gabor transform | Remarks | |
|---|---|---|---|
 |
 |
||
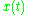| 1 |  |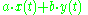
 |
Linearity property |
| 2 |  |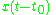
 |
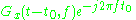Shifting property |
| 3 |  |
 |
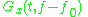Modulation property |
| Remarks | ||
|---|---|---|
| 1 |  |
Power integration property |
| 2 |  |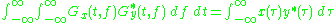
Energy sum property |
| 3 |  |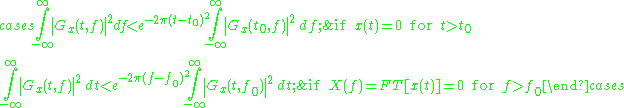
Power decay property |
| 4 |  |
Integration property |
| 5 |  |
Recovery property |
Application and example
The main application of the Gabor transform is used in time frequency analysis. Take the following equation as an example. The input signal has 1Hz frequency component when t ≤ 0 and has 2Hz frequency component when t > 0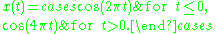But if the total bandwidth available is 5Hz, other frequency bands except x(t) are wasted. Through time frequency analysis by applying the Gabor transform, the available bandwidth can be known and those frequency bands can be used for other applications and bandwidth is saved. The right side picture show the input signal x(t) and the output of the Gabor transform. As our expectation, the frequency distribution can be separate as two parts. One is t ≤ 0 and the other is t > 0. The white part is the frequency band occupied by x(t) and the black part is not used.
See also
- Gabor filterGabor filterIn image processing, a Gabor filter, named after Dennis Gabor, is a linear filter used for edge detection. Frequency and orientation representations of Gabor filters are similar to those of the human visual system, and they have been found to be particularly appropriate for texture representation...
- Gabor atom
- Gabor wavelet
- Time-frequency representationTime-frequency representationA time–frequency representation is a view of a signal represented over both time and frequency. Time–frequency analysis means analysis into the time–frequency domain provided by a TFR...
- Short-time Fourier transformShort-time Fourier transformThe short-time Fourier transform , or alternatively short-term Fourier transform, is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time....
- Wigner distribution functionWigner distribution functionThe Wigner distribution function was first proposed to account for quantum corrections to classical statistical mechanics in 1932 by Eugene Wigner, cf. Wigner quasi-probability distribution....