
Gauss circle problem
Encyclopedia
In mathematics
, the Gauss circle problem is the problem of determining how many integer lattice
points there are in a circle
centred at the origin and with radius
r. The first progress on a solution was made by Carl Friedrich Gauss
, hence its name.
of this circle is given in Cartesian coordinates
by x2 + y2 = r2, the question is equivalently asking how many pairs of integers m and n there are such that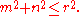
If the answer for a given r is denoted by N(r) then the following list shows the first few values of N(r) for r an integer between 0 and 10:
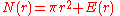
for some error term E(r). Finding a correct upper bound for E(r) is thus the form the problem has taken.
Gauss managed to prove that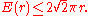
Hardy
and, independently, Landau
found a lower bound by showing that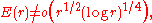
using the little o-notation. It is conjectured that the correct bound is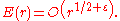
Writing |E(r)| ≤ Crt, the current bounds on t are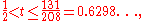
with the lower bound from Hardy and Landau in 1915, and the upper bound proved by Huxley
in 2000.
In 2007, Sylvain Cappell
and Julius Shaneson deposited a paper in the arXiv
claiming to prove the bound of O(r1/2+ε). Kannan Soundararajan
is reported to have found a mistake in the proof.
it can be expressed as: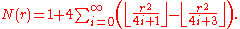
A much simpler sum appears if the sum of squares function r2(n) is defined as the number of ways of writing the number n as the sum of two squares. Then
. Similarly one could extend the question from two dimensions to higher dimensions ( in 3, in 4,
in 5, etc. in 6 and higher), and ask for integer points within a sphere or other objects. If one ignores the geometry and merely considers the problem an algebraic one of Diophantine inequalities then there one could increase the exponents appearing in the problem from squares to cubes, or higher.
integer solutions m, n to the equation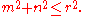
This problem is known as the primitive circle problem, as it involves searching for primitive solutions to the original circle problem. If the number of such solutions is denoted V(r) then the values of V(r) for r taking integer values from 0 to 10 are
Using the same ideas as the usual Gauss circle problem and the fact that the probability that two integers are coprime is 6/π2, it is relatively straightforward to show that
As with the usual circle problem, the problematic part of the primitive circle problem is reducing the exponent in the error term. At present the best known exponent is 221/304 + ε if one assumes the Riemann hypothesis
. Without assuming the Riemann hypothesis, the best known upper bound is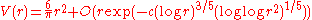
for a positive constant c. In particular, no bound on the error term of the form 1 − ε for any ε > 0 is currently known that does not assume the Riemann Hypothesis.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Gauss circle problem is the problem of determining how many integer lattice
Integer lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
points there are in a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
centred at the origin and with radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
r. The first progress on a solution was made by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
, hence its name.
The problem
Consider a circle in R2 with centre at the origin and radius r ≥ 0. Gauss' circle problem asks how many points there are inside this circle of the form (m,n) where m and n are both integers. Since the equationEquation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
of this circle is given in Cartesian coordinates
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
by x2 + y2 = r2, the question is equivalently asking how many pairs of integers m and n there are such that
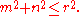
If the answer for a given r is denoted by N(r) then the following list shows the first few values of N(r) for r an integer between 0 and 10:
- 1, 5, 13, 29, 49, 81, 113, 149, 197, 253, 317 .
Bounds on a solution and conjecture
The area inside a circle of radius r is given by πr2, and since a square of area 1 in R2 contains one integer point, the expected answer to the problem could be about πr2. In fact it should be slightly higher than this, since circles are more efficient at enclosing space than squares. So in fact it should be expected that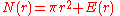
for some error term E(r). Finding a correct upper bound for E(r) is thus the form the problem has taken.
Gauss managed to prove that
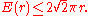
Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and, independently, Landau
Edmund Landau
Edmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
found a lower bound by showing that
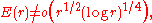
using the little o-notation. It is conjectured that the correct bound is
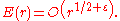
Writing |E(r)| ≤ Crt, the current bounds on t are
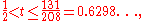
with the lower bound from Hardy and Landau in 1915, and the upper bound proved by Huxley
Martin Huxley
Martin Neil Huxley is a British mathematician, working in the field of analytic number theory.He was awarded a PhD from the University of Cambridge in 1970, the year after his supervisor Harold Davenport had died...
in 2000.
In 2007, Sylvain Cappell
Sylvain Cappell
Sylvain Edward Cappell , a Belgian American mathematician and former student of William Browder at Princeton University, is a topologist who has spent most of his career at the Courant Institute of Mathematical Sciences at NYU, where he is now the Silver Professor of Mathematics.He was born in...
and Julius Shaneson deposited a paper in the arXiv
ArXiv
The arXiv |Chi]], χ) is an archive for electronic preprints of scientific papers in the fields of mathematics, physics, astronomy, computer science, quantitative biology, statistics, and quantitative finance which can be accessed online. In many fields of mathematics and physics, almost all...
claiming to prove the bound of O(r1/2+ε). Kannan Soundararajan
Kannan Soundararajan
Kannan Soundararajan is an Indian mathematician. He currently is a professor of mathematics at Stanford University. Before moving to Stanford in 2006, he was a faculty at University of Michigan where he pursued his undergraduate studies...
is reported to have found a mistake in the proof.
Exact forms
The value of N(r) can be given by several series. In terms of a sum involving the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
it can be expressed as:
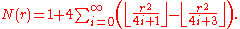
A much simpler sum appears if the sum of squares function r2(n) is defined as the number of ways of writing the number n as the sum of two squares. Then

Generalisations
Although the original problem asks for integer lattice points in a circle, there is no reason not to consider other shapes or conics, indeed Dirichlet's divisor problem is the equivalent problem where the circle is replaced by the rectangular hyperbolaHyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. Similarly one could extend the question from two dimensions to higher dimensions ( in 3, in 4,
in 5, etc. in 6 and higher), and ask for integer points within a sphere or other objects. If one ignores the geometry and merely considers the problem an algebraic one of Diophantine inequalities then there one could increase the exponents appearing in the problem from squares to cubes, or higher.
The primitive circle problem
Another generalisation is to calculate the number of coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
integer solutions m, n to the equation
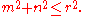
This problem is known as the primitive circle problem, as it involves searching for primitive solutions to the original circle problem. If the number of such solutions is denoted V(r) then the values of V(r) for r taking integer values from 0 to 10 are
- 0, 4, 8, 16, 32, 48, 72, 88, 120, 152, 192.
Using the same ideas as the usual Gauss circle problem and the fact that the probability that two integers are coprime is 6/π2, it is relatively straightforward to show that

As with the usual circle problem, the problematic part of the primitive circle problem is reducing the exponent in the error term. At present the best known exponent is 221/304 + ε if one assumes the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
. Without assuming the Riemann hypothesis, the best known upper bound is
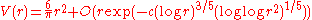
for a positive constant c. In particular, no bound on the error term of the form 1 − ε for any ε > 0 is currently known that does not assume the Riemann Hypothesis.

