
Gaussian polar coordinates
Encyclopedia
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In each of these spheres, every point can be carried to any other by an appropriate rotation about the center of symmetry.
There are several different types of coordinate chart which are adapted to this family of nested spheres, each introducing a different kind of distortion. The best known alternative is the Schwarzschild chart
, which correctly represents distances within each sphere, but (in general) distorts radial distances and angles. Another popular choice is the isotropic chart
, which correctly represents angles (but in general distorts both radial and transverse distances). A third choice is the Gaussian polar chart, which correctly represents radial distances, but distorts transverse distances and angles. In all three possibilities, the nested geometric spheres are represented by coordinate spheres, so we can say that their roundness is correctly represented.
takes the form
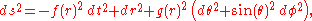
Depending on context, it may be appropriate to regard f, g as undetermined functions of the radial coordinate. Alternatively, we can plug in specific functions (possibly depending on some parameters) to obtain an isotropic coordinate chart on a specific Lorentzian spacetime.
There are several different types of coordinate chart which are adapted to this family of nested spheres, each introducing a different kind of distortion. The best known alternative is the Schwarzschild chart
Schwarzschild coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
, which correctly represents distances within each sphere, but (in general) distorts radial distances and angles. Another popular choice is the isotropic chart
Isotropic coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. There are several different types of coordinate chart which are adapted to this family of nested spheres; the best known is the Schwarzschild chart, but the isotropic chart is also often...
, which correctly represents angles (but in general distorts both radial and transverse distances). A third choice is the Gaussian polar chart, which correctly represents radial distances, but distorts transverse distances and angles. In all three possibilities, the nested geometric spheres are represented by coordinate spheres, so we can say that their roundness is correctly represented.
Definition
In a Gaussian polar chart (on a static spherically symmetric spacetime), the line elementLine element
A line element ds in mathematics can most generally be thought of as the change in a position vector in an affine space expressing the change of the arc length. An easy way of visualizing this relationship is by parametrizing the given curve by Frenet–Serret formulas...
takes the form

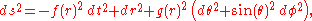
Depending on context, it may be appropriate to regard f, g as undetermined functions of the radial coordinate. Alternatively, we can plug in specific functions (possibly depending on some parameters) to obtain an isotropic coordinate chart on a specific Lorentzian spacetime.
Applications
Gaussian charts are often less convenient than Schwarzschild or isotropic charts. However, they have found occasional application in the theory of static spherically symmetric perfect fluids.See also
- static spacetimeStatic spacetimeIn general relativity, a spacetime is said to be static if it admits a global, non-vanishing, timelike Killing vector field K which is irrotational, i.e., whose orthogonal distribution is involutive...
, - spherically symmetric spacetimeSpherically symmetric spacetimeA spherically symmetric spacetime is a spacetime whose isometry group contains a subgroup which is isomorphic to the group SO and the orbits of this group are 2-dimensional spheres . The isometries are then interpreted as rotations and a spherically symmetric spacetime is often described as one...
, - static spherically symmetric perfect fluidStatic spherically symmetric perfect fluidIn metric theories of gravitation, particularly general relativity, a static spherically symmetric perfect fluid solution is a spacetime equipped with suitable tensor fields which models a static round ball of a fluid with isotropic pressure.Such solutions are often used as idealized models of...
s, - Schwarzschild coordinatesSchwarzschild coordinatesIn the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
, - isotropic coordinatesIsotropic coordinatesIn the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. There are several different types of coordinate chart which are adapted to this family of nested spheres; the best known is the Schwarzschild chart, but the isotropic chart is also often...
, - frame fields in general relativityFrame fields in general relativityIn general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
, for more about frame fields and coframe fields.

