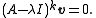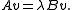Generalized eigenvector
Encyclopedia
In linear algebra
, for a matrix
A, there may not always exist a full set of linearly independent eigenvectors that form a complete basis – a matrix may not be diagonalizable
. This happens when the algebraic multiplicity of at least one eigenvalue λ is greater than its geometric multiplicity (the nullity
of the matrix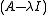 , or the dimension
, or the dimension
of its nullspace). In such cases, a generalized eigenvector of A is a nonzero vector
v, which is associated with λ having algebraic multiplicity k ≥1, satisfying
The set of all generalized eigenvectors for a given λ form the generalized eigenspace for λ.
Ordinary eigenvectors and eigenspaces are obtained for k=1.
of a defective matrix
, which is a matrix in which there are fewer linearly independent eigenvectors than eigenvalues (counting multiplicity). Over an algebraically closed field, the generalized eigenvectors do allow choosing a complete basis, as follows from the Jordan form of a matrix.
In particular, suppose that an eigenvalue λ of a matrix A has an algebraic multiplicity m but fewer corresponding eigenvectors. We form a sequence of m eigenvectors and generalized eigenvectors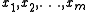 that are linearly independent and satisfy
that are linearly independent and satisfy
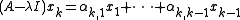
for some coefficients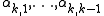 , for
, for 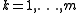 . It follows that
. It follows that
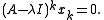
The vectors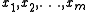 can always be chosen, but are not uniquely determined by the above relations. If the geometric multiplicity (dimension of the eigenspace) of λ is p, one can choose the first p vectors to be eigenvectors, but the remaining m − p vectors are only generalized eigenvectors.
can always be chosen, but are not uniquely determined by the above relations. If the geometric multiplicity (dimension of the eigenspace) of λ is p, one can choose the first p vectors to be eigenvectors, but the remaining m − p vectors are only generalized eigenvectors.
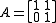
Then there is one eigenvalue λ=1 with an algebraic multiplicity m of 2.
There are several ways to see that there will be one generalized eigenvector necessary. Easiest is to notice that this matrix is in Jordan normal form, but is not diagonal, meaning that this is not a diagonalizable matrix. Since there is 1 superdiagonal entry, there will be one generalized eigenvector (or you could note that the vector space is of dimension 2, so there can be only one generalized eigenvector). Alternatively, you could compute the dimension of the nullspace of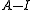 to be p=1, and thus there are m-p=1 generalized eigenvectors.
to be p=1, and thus there are m-p=1 generalized eigenvectors.
Computing the ordinary eigenvector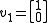 is left to the reader (see the eigenvector page for examples). Using this eigenvector, we compute the generalized eigenvector
is left to the reader (see the eigenvector page for examples). Using this eigenvector, we compute the generalized eigenvector 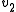 by solving
by solving
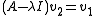
Writing out the values: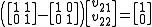
This simplifies to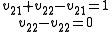
This simplifies to
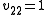
And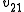 has no restrictions and thus can be any scalar. So the generalized eigenvector is
has no restrictions and thus can be any scalar. So the generalized eigenvector is 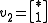 , where the * indicates any value is fine. Usually picking 0 is easiest.
, where the * indicates any value is fine. Usually picking 0 is easiest.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, for a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A, there may not always exist a full set of linearly independent eigenvectors that form a complete basis – a matrix may not be diagonalizable
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
. This happens when the algebraic multiplicity of at least one eigenvalue λ is greater than its geometric multiplicity (the nullity
Nullity
Nullity may refer to:* Nullity , a legal declaration that no marriage had ever come into being* Nullity, the dimension of the null space of a mathematical operator or matrix...
of the matrix
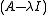 , or the dimension
, or the dimensionDimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of its nullspace). In such cases, a generalized eigenvector of A is a nonzero vector
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
v, which is associated with λ having algebraic multiplicity k ≥1, satisfying
The set of all generalized eigenvectors for a given λ form the generalized eigenspace for λ.
Ordinary eigenvectors and eigenspaces are obtained for k=1.
For defective matrices
Generalized eigenvectors are needed to form a complete basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of a defective matrix
Defective matrix
In linear algebra, a defective matrix is a square matrix that does not have a complete basis of eigenvectors, and is therefore not diagonalizable. In particular, an n × n matrix is defective if and only if it does not have n linearly independent eigenvectors...
, which is a matrix in which there are fewer linearly independent eigenvectors than eigenvalues (counting multiplicity). Over an algebraically closed field, the generalized eigenvectors do allow choosing a complete basis, as follows from the Jordan form of a matrix.
In particular, suppose that an eigenvalue λ of a matrix A has an algebraic multiplicity m but fewer corresponding eigenvectors. We form a sequence of m eigenvectors and generalized eigenvectors
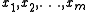 that are linearly independent and satisfy
that are linearly independent and satisfy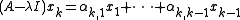
for some coefficients
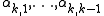 , for
, for 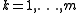 . It follows that
. It follows that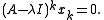
The vectors
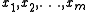 can always be chosen, but are not uniquely determined by the above relations. If the geometric multiplicity (dimension of the eigenspace) of λ is p, one can choose the first p vectors to be eigenvectors, but the remaining m − p vectors are only generalized eigenvectors.
can always be chosen, but are not uniquely determined by the above relations. If the geometric multiplicity (dimension of the eigenspace) of λ is p, one can choose the first p vectors to be eigenvectors, but the remaining m − p vectors are only generalized eigenvectors.Example
If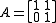
Then there is one eigenvalue λ=1 with an algebraic multiplicity m of 2.
There are several ways to see that there will be one generalized eigenvector necessary. Easiest is to notice that this matrix is in Jordan normal form, but is not diagonal, meaning that this is not a diagonalizable matrix. Since there is 1 superdiagonal entry, there will be one generalized eigenvector (or you could note that the vector space is of dimension 2, so there can be only one generalized eigenvector). Alternatively, you could compute the dimension of the nullspace of
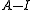 to be p=1, and thus there are m-p=1 generalized eigenvectors.
to be p=1, and thus there are m-p=1 generalized eigenvectors.Computing the ordinary eigenvector
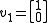 is left to the reader (see the eigenvector page for examples). Using this eigenvector, we compute the generalized eigenvector
is left to the reader (see the eigenvector page for examples). Using this eigenvector, we compute the generalized eigenvector 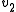 by solving
by solving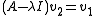
Writing out the values:
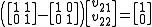
This simplifies to
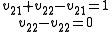
This simplifies to
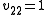
And
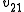 has no restrictions and thus can be any scalar. So the generalized eigenvector is
has no restrictions and thus can be any scalar. So the generalized eigenvector is 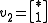 , where the * indicates any value is fine. Usually picking 0 is easiest.
, where the * indicates any value is fine. Usually picking 0 is easiest.Other meanings of the term
- The usage of generalized eigenfunction differs from this; it is part of the theory of rigged Hilbert spaceRigged Hilbert spaceIn mathematics, a rigged Hilbert space is a construction designed to link the distribution and square-integrable aspects of functional analysis. Such spaces were introduced to study spectral theory in the broad sense...
s, so that for a linear operator on a function spaceFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
this may be something different.
- One can also use the term generalized eigenvector for an eigenvector of the generalized eigenvalue problem