
Defective matrix
Encyclopedia
In linear algebra
, a defective matrix is a square matrix that does not have a complete basis
of eigenvectors, and is therefore not diagonalizable
. In particular, an n × n matrix is defective if and only if it does not have n linearly independent eigenvectors. A complete basis is formed by augmenting the eigenvectors with generalized eigenvector
s, which are necessary for solving defective systems of ordinary differential equation
s and other problems.
A defective matrix always has fewer than n distinct eigenvalues, since distinct eigenvalues always have linearly independent eigenvectors. In particular, a defective matrix has one or more eigenvalues λ with algebraic multiplicity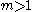 (that is, they are multiple roots of the characteristic polynomial
(that is, they are multiple roots of the characteristic polynomial
), but fewer than m linearly independent eigenvectors associated with λ. However, every eigenvalue with multiplicity m always has m linearly independent generalized eigenvectors.
A Hermitian matrix (or the special case of a real symmetric matrix) or a unitary matrix is never defective; more generally, a normal matrix
(which includes Hermitian and unitary as special cases) is never defective.
of size 2×2 or larger is defective. For example, the n × n Jordan block,
has an eigenvalue, λ, with multiplicity n, but only one distinct eigenvector,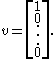
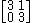
which has a double eigenvalue of 3 but only one distinct eigenvector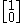
(and constant multiples thereof).
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a defective matrix is a square matrix that does not have a complete basis
Basis function
In mathematics, a basis function is an element of a particular basis for a function space. Every continuous function in the function space can be represented as a linear combination of basis functions, just as every vector in a vector space can be represented as a linear combination of basis...
of eigenvectors, and is therefore not diagonalizable
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
. In particular, an n × n matrix is defective if and only if it does not have n linearly independent eigenvectors. A complete basis is formed by augmenting the eigenvectors with generalized eigenvector
Generalized eigenvector
In linear algebra, for a matrix A, there may not always exist a full set of linearly independent eigenvectors that form a complete basis – a matrix may not be diagonalizable. This happens when the algebraic multiplicity of at least one eigenvalue λ is greater than its geometric multiplicity...
s, which are necessary for solving defective systems of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s and other problems.
A defective matrix always has fewer than n distinct eigenvalues, since distinct eigenvalues always have linearly independent eigenvectors. In particular, a defective matrix has one or more eigenvalues λ with algebraic multiplicity
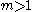 (that is, they are multiple roots of the characteristic polynomial
(that is, they are multiple roots of the characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
), but fewer than m linearly independent eigenvectors associated with λ. However, every eigenvalue with multiplicity m always has m linearly independent generalized eigenvectors.
A Hermitian matrix (or the special case of a real symmetric matrix) or a unitary matrix is never defective; more generally, a normal matrix
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
(which includes Hermitian and unitary as special cases) is never defective.
Jordan block
Any Jordan blockJordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
of size 2×2 or larger is defective. For example, the n × n Jordan block,

has an eigenvalue, λ, with multiplicity n, but only one distinct eigenvector,
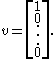
Example
A simple example of a defective matrix is: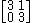
which has a double eigenvalue of 3 but only one distinct eigenvector
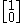
(and constant multiples thereof).

