Generic scalar transport equation
Encyclopedia
The generic scalar transport equation is a general partial differential equation
that describes transport phenomena
such as heat transfer
, mass transfer
, fluid dynamics
(momentum
transfer), etc. A general form of the equation is
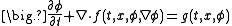
where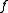
is called the flux, and 
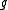is called the source.
All the transfer processes express a certain conservation principle. In this respect, any differential equation addresses a certain quantity as its dependent variable and thus expresses the balance between the phenomena affecting the evolution of this quantity. For example, the temperature
of a fluid in a heated pipe is affected by convection
due to the solid-fluid interface, and due to the fluid-fluid interaction. Furthermore, temperature is also diffused inside the fluid. For a steady-state problem, with the absence of sources
, a differential equation governing the temperature will express a balance between convection and diffusion
.
A brief inspection of the equations governing various transport phenomena reveal that all of these equations can be put into a generic form thus allowing a systematic approach for a computer simulation
. For example, the conservation equation of a concentration
of a substance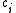
is
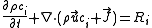
where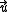
denotes the velocity field, 
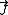denotes the diffusion flux of the chemical species, and 
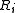denotes the rate of generation of 
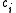caused by chemical reaction.
The x-momentum equation for a Newtonian fluid
can be written as
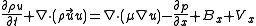
where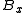
is the body force in the x-direction and 
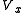includes the viscous
terms that are not expressed by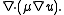
Upon inspection of the above equations, it can be inferred that all the dependent variables seem to obey a generalized conservation principle
. If the dependent variable (scalar or vector) is denoted by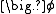
, the generic differential equation is
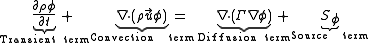
where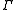
is the diffusion coefficient, or diffusivity.
The objective of all discretization
techniques (finite difference
, finite element, finite volume
, boundary element
, etc.) is to devise a mathematical formulation to transform each of these terms into an algebraic equation. Once applied to all control volumes in a given mesh, we obtain a full linear system of equations that needs to be solved.
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
that describes transport phenomena
Transport Phenomena
Transport Phenomena is the first textbook that is about transport phenomena. It is specifically designed for chemical engineering students...
such as heat transfer
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
, mass transfer
Mass transfer
Mass transfer is the net movement of mass from one location, usually meaning a stream, phase, fraction or component, to another. Mass transfer occurs in many processes, such as absorption, evaporation, adsorption, drying, precipitation, membrane filtration, and distillation. Mass transfer is used...
, fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
(momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
transfer), etc. A general form of the equation is
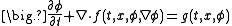
where
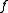is called the flux, and 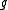is called the source.All the transfer processes express a certain conservation principle. In this respect, any differential equation addresses a certain quantity as its dependent variable and thus expresses the balance between the phenomena affecting the evolution of this quantity. For example, the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
of a fluid in a heated pipe is affected by convection
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
due to the solid-fluid interface, and due to the fluid-fluid interaction. Furthermore, temperature is also diffused inside the fluid. For a steady-state problem, with the absence of sources
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, a differential equation governing the temperature will express a balance between convection and diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
.
A brief inspection of the equations governing various transport phenomena reveal that all of these equations can be put into a generic form thus allowing a systematic approach for a computer simulation
Computer simulation
A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...
. For example, the conservation equation of a concentration
Concentration
In chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. Four types can be distinguished: mass concentration, molar concentration, number concentration, and volume concentration...
of a substance
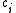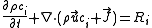
iswhere
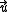denotes the velocity field, 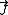denotes the diffusion flux of the chemical species, and 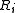denotes the rate of generation of 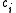caused by chemical reaction.The x-momentum equation for a Newtonian fluid
Newtonian fluid
A Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:...
can be written as
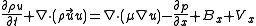
where
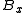is the body force in the x-direction and 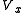includes the viscousViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
terms that are not expressed by
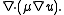
Upon inspection of the above equations, it can be inferred that all the dependent variables seem to obey a generalized conservation principle
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
. If the dependent variable (scalar or vector) is denoted by
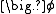, the generic differential equation is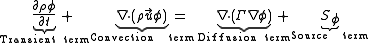where
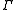is the diffusion coefficient, or diffusivity.- The transient term,
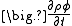, accounts for the accumulation of 
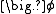in the concerned control volumeControl volumeIn fluid mechanics and thermodynamics, a control volume is a mathematical abstraction employed in the process of creating mathematical models of physical processes. In an inertial frame of reference, it is a volume fixed in space or moving with constant velocity through which the fluid flows...
. - The convection term,
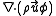, accounts for the transport of 
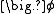due to the existence of the velocity field (note the velocity 
multiplying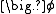 
). - The diffusion term,
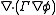, accounts for the transport of 
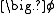due to its gradients. - The source term,
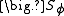, accounts for any sources or sinks that either create or destroy 
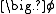. Any extra terms that cannot be cast into the convection or diffusion terms are considered as source terms.
The objective of all discretization
Discretization
In mathematics, discretization concerns the process of transferring continuous models and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers...
techniques (finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
, finite element, finite volume
Finite volume method
The finite volume method is a method for representing and evaluating partial differential equations in the form of algebraic equations [LeVeque, 2002; Toro, 1999]....
, boundary element
Boundary element method
The boundary element method is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations . It can be applied in many areas of engineering and science including fluid mechanics, acoustics, electromagnetics, and fracture...
, etc.) is to devise a mathematical formulation to transform each of these terms into an algebraic equation. Once applied to all control volumes in a given mesh, we obtain a full linear system of equations that needs to be solved.
Scalar transport equation in financial mathematics
Some equations that governs the dynamics of financial derivatives in financial markets can be also categorized as generic scalar transport equations. Examples include the Black-Scholes equation.See also
- Continuity equationContinuity equationA continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
- Buckley–Leverett equationBuckley–Leverett equationIn fluid dynamics, the Buckley–Leverett equation is a transport equation used to model two-phase flow in porous media. The Buckley–Leverett equation or the Buckley–Leverett displacement can be interpreted as a way of incorporating the microscopic effects to due capillary pressure in two-phase flow...
- Convection diffusion equation