Finite volume method
Encyclopedia
The finite volume method is a method for representing and evaluating partial differential equation
s in the form of algebraic equations [LeVeque, 2002; Toro, 1999].
Similar to the finite difference method
or finite element method
, values are calculated at discrete places on a meshed geometry. "Finite volume" refers to the small volume surrounding each node point on a mesh. In the finite volume method, volume integrals in a partial differential equation that contain a divergence
term are converted to surface integral
s, using the divergence theorem
. These terms are then evaluated as fluxes at the surfaces of each finite volume. Because the flux entering a given volume is identical to that leaving the adjacent volume, these methods are conservative
. Another advantage of the finite volume method is that it is easily formulated to allow for unstructured meshes. The method is used in many computational fluid dynamics
packages.
problem defined by the following partial differential equation
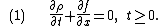
Here,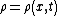
represents the state variable and 
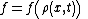represents the flux
or flow of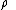
. Conventionally, positive 
represents flow to the right while negative 
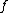represents flow to the left. If we assume that equation (1) represents a flowing medium of constant area, we can sub-divide the spatial domain, 
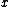, into finite volumes or cells with cell centres indexed as 
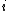. For a particular cell, 
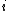, we can define the volume average value of 
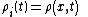at time 
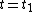and 
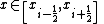, as
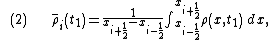
and at time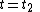
as,
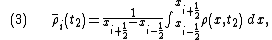
where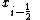
and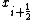 
represent locations of the upstream and downstream faces or edges respectively of the 
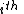cell.
Integrating equation (1) in time, we have:
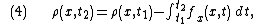
where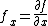
.
To obtain the volume average of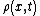
at time 
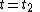, we integrate 
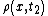over the cell volume, 
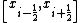and divide the result by 
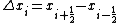, i.e.
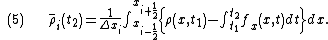
We assume that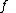
is well behaved and that we can reverse the order of integration. Also, recall that flow is normal to the unit area of the cell. Now, since in one dimension 
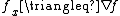, we can apply the divergence theorem
, i.e.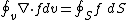
, and substitute for the volume integral of the divergence
with the values of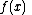
evaluated at the cell surface (edges 
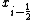and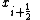 
) of the finite volume as follows:
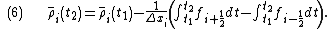
where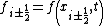
.
We can therefore derive a semi-discrete numerical scheme for the above problem with cell centres indexed as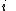
, and with cell edge fluxes indexed as 
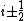, by differentiating (6) with respect to time to obtain:
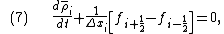
where values for the edge fluxes,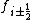
, can be reconstructed by interpolation or extrapolation of the cell averages. Equation (7) is exact for the volume averages; i.e., no approximations have been made during its derivation.
problem, represented by the following PDE
,
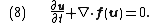
Here,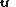
represents a vector of states and 
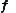represents the corresponding flux
tensor. Again we can sub-divide the spatial domain into finite volumes or cells. For a particular cell,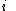
, we take the volume integral over the total volume of the cell, 
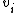, which gives,
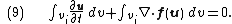
On integrating the first term to get the volume average and applying the divergence theorem to the second, this yields
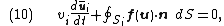
where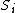
represents the total surface area of the cell and 
is a unit vector normal to the surface and pointing outward. So, finally, we are able to present the general result equivalent to (7), i.e.
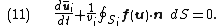
Again, values for the edge fluxes can be reconstructed by interpolation or extrapolation of the cell averages. The actual numerical scheme will depend upon problem geometry and mesh construction. MUSCL
reconstruction is often used in high resolution scheme
s where shocks or discontinuities are present in the solution.
Finite volume schemes are conservative as cell averages change through the edge fluxes. In other words, one cell's loss is another cell's gain!
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s in the form of algebraic equations [LeVeque, 2002; Toro, 1999].
Similar to the finite difference method
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
or finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
, values are calculated at discrete places on a meshed geometry. "Finite volume" refers to the small volume surrounding each node point on a mesh. In the finite volume method, volume integrals in a partial differential equation that contain a divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
term are converted to surface integral
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
s, using the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
. These terms are then evaluated as fluxes at the surfaces of each finite volume. Because the flux entering a given volume is identical to that leaving the adjacent volume, these methods are conservative
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
. Another advantage of the finite volume method is that it is easily formulated to allow for unstructured meshes. The method is used in many computational fluid dynamics
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
packages.
1D example
Consider a simple 1D advectionAdvection
Advection, in chemistry, engineering and earth sciences, is a transport mechanism of a substance, or a conserved property, by a fluid, due to the fluid's bulk motion in a particular direction. An example of advection is the transport of pollutants or silt in a river. The motion of the water carries...
problem defined by the following partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
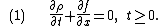
Here,
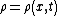represents the state variable and 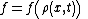represents the fluxFlux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
or flow of
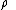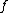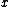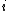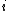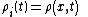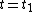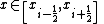. Conventionally, positive represents flow to the right while negative represents flow to the left. If we assume that equation (1) represents a flowing medium of constant area, we can sub-divide the spatial domain, , into finite volumes or cells with cell centres indexed as . For a particular cell, , we can define the volume average value of at time and , as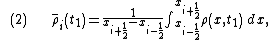and at time
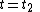as,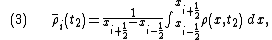where
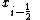and 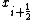represent locations of the upstream and downstream faces or edges respectively of the 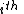cell.Integrating equation (1) in time, we have:
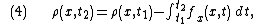
where
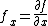.To obtain the volume average of
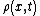at time 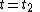, we integrate 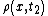over the cell volume, 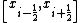and divide the result by 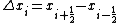, i.e.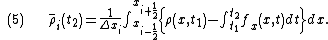We assume that
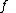is well behaved and that we can reverse the order of integration. Also, recall that flow is normal to the unit area of the cell. Now, since in one dimension 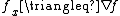, we can apply the divergence theoremDivergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
, i.e.
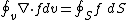, and substitute for the volume integral of the divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
with the values of
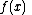evaluated at the cell surface (edges 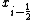and 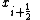) of the finite volume as follows: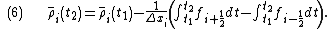where
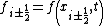.We can therefore derive a semi-discrete numerical scheme for the above problem with cell centres indexed as
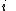, and with cell edge fluxes indexed as 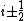, by differentiating (6) with respect to time to obtain: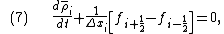where values for the edge fluxes,
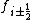, can be reconstructed by interpolation or extrapolation of the cell averages. Equation (7) is exact for the volume averages; i.e., no approximations have been made during its derivation.General conservation law
We can also consider the general conservation lawConservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
problem, represented by the following PDE
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
,
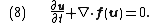
Here,
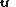represents a vector of states and 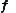represents the corresponding fluxFlux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
tensor. Again we can sub-divide the spatial domain into finite volumes or cells. For a particular cell,
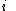, we take the volume integral over the total volume of the cell, 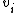, which gives,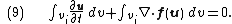On integrating the first term to get the volume average and applying the divergence theorem to the second, this yields
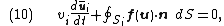
where
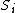represents the total surface area of the cell and is a unit vector normal to the surface and pointing outward. So, finally, we are able to present the general result equivalent to (7), i.e.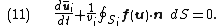Again, values for the edge fluxes can be reconstructed by interpolation or extrapolation of the cell averages. The actual numerical scheme will depend upon problem geometry and mesh construction. MUSCL
MUSCL scheme
In the study of partial differential equations, the MUSCL scheme is a finite volume method that can provide highly accurate numerical solutions for a given system, even in cases where the solutions exhibit shocks, discontinuities, or large gradients...
reconstruction is often used in high resolution scheme
High resolution scheme
High-resolution schemes are used in the numerical solution of partial differential equations where high accuracy is required in the presence of shocks or discontinuities...
s where shocks or discontinuities are present in the solution.
Finite volume schemes are conservative as cell averages change through the edge fluxes. In other words, one cell's loss is another cell's gain!
See also
- Flux limiterFlux limiterFlux limiters are used in high resolution schemes – numerical schemes used to solve problems in science and engineering, particularly fluid dynamics, described by partial differential equations...
- Godunov's theoremGodunov's theoremIn numerical analysis and computational fluid dynamics, Godunov's theorem — also known as Godunov's order barrier theorem — is a mathematical theorem important in the development of the theory of high resolution schemes for the numerical solution of partial differential equations.The theorem states...
- High-resolution scheme
- KIVA (Software)KIVA (software)KIVA is a family of Fortran-based Computational Fluid Dynamics software developed by Los Alamos National Laboratory . The software predicts complex fuel and air flows as well as ignition, combustion, and pollutant-formation processes in engines...
- MIT General Circulation ModelMIT General Circulation ModelThe MIT General Circulation Model is a numerical computer code that solves the equations of motion governing the ocean or Earth's atmosphere using the finite volume method. It was developed at the Massachusetts Institute of Technology and was one of the first non-hydrostatic models of the ocean...
- MUSCL schemeMUSCL schemeIn the study of partial differential equations, the MUSCL scheme is a finite volume method that can provide highly accurate numerical solutions for a given system, even in cases where the solutions exhibit shocks, discontinuities, or large gradients...
- Sergei K. GodunovSergei K. GodunovSergei Konstantinovich Godunov is professor at the Sobolev Institute of Mathematics of the Russian Academy of Sciences in Novosibirsk, Russia....
- Total variation diminishingTotal variation diminishingIn numerical methods, total variation diminishing is a property of certain discretization schemes used to solve hyperbolic partial differential equations...
Further reading
- Hirsch, C. (1990), Numerical Computation of Internal and External Flows, Volume 2: Computational Methods for Inviscid and Viscous Flows, Wiley.
- Laney, Culbert B. (1998), Computational Gas Dynamics, Cambridge University Press.
- LeVeque, Randall (1990), Numerical Methods for Conservation Laws, ETH Lectures in Mathematics Series, Birkhauser-Verlag.
- Patankar, Suhas V. (1980), Numerical Heat Transfer and Fluid Flow, Hemisphere.
- Tannehill, John C., et al., (1997), Computational Fluid mechanics and Heat Transfer, 2nd Ed., Taylor and Francis.
- Wesseling, Pieter (2001), Principles of Computational Fluid Dynamics, Springer-Verlag.
External links
- The finite volume method by R. Eymard, T Gallouët and R. Herbin, update of the article published in Handbook of Numerical Analysis, 2000
- The Finite Volume Method (FVM) - An introduction by Oliver Rübenkönig of Albert Ludwigs University of Freiburg, available under the GFDL.
- FiPy: A Finite Volume PDE Solver Using Python from NIST.
- CLAWPACK: a software package designed to compute numerical solutions to hyperbolic partial differential equations using a wave propagation approach