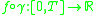Geodesic convexity
Encyclopedia
In mathematics
— specifically, in Riemannian geometry
— geodesic convexity is a natural generalization of convexity for sets
and functions
to Riemannian manifold
s. It is common to drop the prefix "geodesic" and refer simply to "convexity" of a set or function.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
— geodesic convexity is a natural generalization of convexity for sets
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
and functions
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
to Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s. It is common to drop the prefix "geodesic" and refer simply to "convexity" of a set or function.
Definitions
Let (M, g) be a Riemannian manifold.- A subset C of M is said to be a geodesically convex set if, given any two points in C, there is a minimizing geodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
contained within C that joins those two points.
- Let C be a geodesically convex subset of M. A function f : C → R is said to be a (strictly) geodesically convex function if the composition
- is a (strictly) convex function in the usual sense for every unit speed geodesic arc γ : [0, T] → M contained within C.
Properties
- A geodesically convex (subset of a) Riemannian manifold is also a convex metric spaceConvex metric spaceIn mathematics, convex metric spaces are, intuitively, metric spaces with the property any "segment" joining two points in that space has other points in it besides the endpoints....
with respect to the geodesic distance.
Examples
- A subset of n-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
En with its usual flat metric is geodesically convex if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is convex in the usual sense, and similarly for functions. - The "northern hemisphere" of the 2-dimensional sphere S2 with its usual metric is geodesically convex. However, the subset A of S2 consisting of those points with latitudeLatitudeIn geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
further north than 45° south is not geodesically convex, since the geodesic (great circleGreat circleA great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
) joining two points on the southern boundary of A may well leave A (e.g. in the case of two points 180° apart in longitudeLongitudeLongitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
, in which case the geodesic arc passes over the south pole).