
Gibbons-Hawking effect
Encyclopedia
The Gibbons–Hawking effect is the statement that a temperature
can be associated to each solution of the Einstein field equations
that contains a causal horizon. It is named after Gary Gibbons
and Stephen William Hawking.
The term "causal horizon" does not necessarily refer to event horizon
s only, but could also stand for the horizon of the visible universe, for instance.
For example, Schwarzschild spacetime
contains an event horizon and so can be associated a temperature. In the case of Schwarzschild spacetime this is the temperature of a black hole of mass
of a black hole of mass  , satisfying
, satisfying 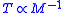 (see also Hawking radiation
(see also Hawking radiation
).
A second example is de Sitter space
which contains a particle horizon. In this case the temperature is proportional to the Hubble parameter
is proportional to the Hubble parameter  , i.e.
, i.e.  .
.
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
can be associated to each solution of the Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
that contains a causal horizon. It is named after Gary Gibbons
Gary Gibbons
Gary William Gibbons , FRS, is a British theoretical physicist. Gibbons studied in Cambridge,where in 1969 he became a research student under the supervision of Dennis Sciama. When Sciama moved to Oxford, he became a student of Stephen Hawking, obtaining his PhD from Cambridge in 1973...
and Stephen William Hawking.
The term "causal horizon" does not necessarily refer to event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
s only, but could also stand for the horizon of the visible universe, for instance.
For example, Schwarzschild spacetime
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
contains an event horizon and so can be associated a temperature. In the case of Schwarzschild spacetime this is the temperature
 of a black hole of mass
of a black hole of mass  , satisfying
, satisfying 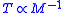 (see also Hawking radiation
(see also Hawking radiationHawking radiation
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
).
A second example is de Sitter space
De Sitter space
In mathematics and physics, a de Sitter space is the analog in Minkowski space, or spacetime, of a sphere in ordinary, Euclidean space. The n-dimensional de Sitter space , denoted dS_n, is the Lorentzian manifold analog of an n-sphere ; it is maximally symmetric, has constant positive curvature,...
which contains a particle horizon. In this case the temperature
 is proportional to the Hubble parameter
is proportional to the Hubble parameter  , i.e.
, i.e.  .
.

