De Sitter space
Encyclopedia
In mathematics
and physics
, a de Sitter space is the analog in Minkowski space
, or spacetime, of a sphere in ordinary, Euclidean space
. The n-dimensional de Sitter space , denoted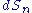
, is the Lorentzian manifold analog of an n-sphere (with its canonical Riemannian metric); it is maximally symmetric, has constant positive curvature
, and is simply-connected for n at least 3.
In the language of general relativity
, de Sitter space is the maximally symmetric, vacuum solution
of Einstein's field equations with a positive (repulsive) cosmological constant
(corresponding to a positive vacuum energy density and negative pressure). When n = 4 (3 space dimensions plus time), it is a cosmological model for the physical universe; see de Sitter universe
.
De Sitter space was discovered by Willem de Sitter
, and, at the same time, independently by Tullio Levi-Civita
.
More recently it has been considered as the setting for special relativity
rather than using Minkowski space and such a formulation is called de Sitter relativity.
of a Minkowski space
of one higher dimension
. Take Minkowski space R1,n with the standard metric
:
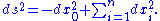
De Sitter space is the submanifold described by the hyperboloid of one sheet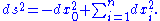
where
is some positive constant with dimensions of length. The metric
on de Sitter space is the metric induced from the ambient Minkowski metric. One can check that the induced metric is nondegenerate and has Lorentzian signature. (Note that if one replaces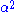
with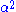 
in the above definition, one obtains a hyperboloid of two sheets. The induced metric in this case is positive-definite, and each sheet is a copy of hyperbolic n-space
.)
De Sitter space can also be defined as the quotient O(1,n)/O(1,n−1) of two indefinite orthogonal groups, which shows that it is a non-Riemannian symmetric space.
Topologically
, de Sitter space is R × Sn−1 (so that that if n ≥ 3 then de Sitter space is simply-connected).
of de Sitter space is the Lorentz group
O(1,n). The metric therefore then has n(n+1)/2 independent Killing vectors and is maximally symmetric. Every maximally symmetric space has constant curvature. The Riemann curvature tensor
of de Sitter is given by
De Sitter space is an Einstein manifold
since the Ricci tensor is proportional to the metric:
This means de Sitter space is a vacuum solution of Einstein's equation with cosmological constant given by
The scalar curvature
of de Sitter space is given by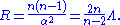
For the case n = 4, we have Λ = 3/α2 and R = 4Λ = 12/α2.
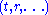for de Sitter as follows: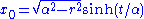
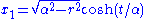
where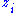
gives the standard embedding the (n−2)-sphere in Rn−1. In these coordinates the de Sitter metric takes the form:
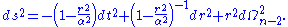
Note that there is a cosmological horizon at
.
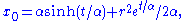
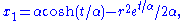
where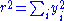
. Then in the 
coordinates metric reads:
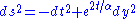
where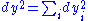
is the flat metric on 
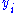's.
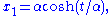
where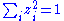
forming a 
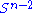with the standard metric 
. Then the metric of the de Sitter space reads
where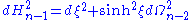
is the metric of a Euclidean hyperbolic space.
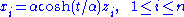
where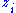
s describe a 
. Then the metric reads:
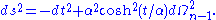
Changing the time variable to the conformal time via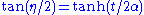
(or equivalently 
) we obtain a metric conformally equivalent to Einstein static universe: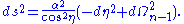
This serves to find the Penrose diagram
of de Sitter space.
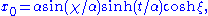
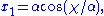
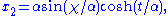
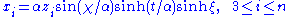
where
s describe a 
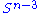. Then the metric reads: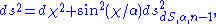
where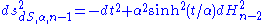
is the metric of an
dimensional de Sitter space with radius of curvature 
in open slicing coordinates. The hyperbolic metric is given by:
This is the analytic continuation of the open slicing coordinates under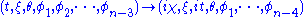
and also switching 
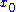and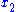 
because they change their timelike/spacelike nature.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a de Sitter space is the analog in Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, or spacetime, of a sphere in ordinary, Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. The n-dimensional de Sitter space , denoted
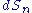, is the Lorentzian manifold analog of an n-sphere (with its canonical Riemannian metric); it is maximally symmetric, has constant positive curvatureScalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
, and is simply-connected for n at least 3.
In the language of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, de Sitter space is the maximally symmetric, vacuum solution
Vacuum solution
A vacuum solution is a solution of a field equation in which the sources of the field are taken to be identically zero. That is, such field equations are written without matter interaction .-Examples:...
of Einstein's field equations with a positive (repulsive) cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
(corresponding to a positive vacuum energy density and negative pressure). When n = 4 (3 space dimensions plus time), it is a cosmological model for the physical universe; see de Sitter universeDe Sitter universe
A de Sitter universe is a cosmological solution to Einstein's field equations of General Relativity which is named after Willem de Sitter. It models the universe as spatially flat and neglects ordinary matter, so the dynamics of the universe are dominated by the cosmological constant, thought to...
.
De Sitter space was discovered by Willem de Sitter
Willem de Sitter
Willem de Sitter was a Dutch mathematician, physicist and astronomer.-Life and work:Born in Sneek, De Sitter studied mathematics at the University of Groningen and then joined the Groningen astronomical laboratory. He worked at the Cape Observatory in South Africa...
, and, at the same time, independently by Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
.
More recently it has been considered as the setting for special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
rather than using Minkowski space and such a formulation is called de Sitter relativity.
Definition
De Sitter space can be defined as a submanifoldSubmanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of a Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
of one higher dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
. Take Minkowski space R1,n with the standard metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
:
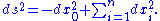
De Sitter space is the submanifold described by the hyperboloid of one sheet
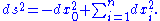
where
is some positive constant with dimensions of length. The metricMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
on de Sitter space is the metric induced from the ambient Minkowski metric. One can check that the induced metric is nondegenerate and has Lorentzian signature. (Note that if one replaces
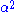with 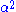in the above definition, one obtains a hyperboloid of two sheets. The induced metric in this case is positive-definite, and each sheet is a copy of hyperbolic n-spaceHyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
.)
De Sitter space can also be defined as the quotient O(1,n)/O(1,n−1) of two indefinite orthogonal groups, which shows that it is a non-Riemannian symmetric space.
Topologically
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, de Sitter space is R × Sn−1 (so that that if n ≥ 3 then de Sitter space is simply-connected).
Properties
The isometry groupIsometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
of de Sitter space is the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
O(1,n). The metric therefore then has n(n+1)/2 independent Killing vectors and is maximally symmetric. Every maximally symmetric space has constant curvature. The Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
of de Sitter is given by
De Sitter space is an Einstein manifold
Einstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
since the Ricci tensor is proportional to the metric:
This means de Sitter space is a vacuum solution of Einstein's equation with cosmological constant given by
The scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
of de Sitter space is given by
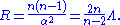
For the case n = 4, we have Λ = 3/α2 and R = 4Λ = 12/α2.
Static coordinates
We can introduce static coordinatesStatic spacetime
In general relativity, a spacetime is said to be static if it admits a global, non-vanishing, timelike Killing vector field K which is irrotational, i.e., whose orthogonal distribution is involutive...
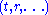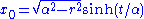
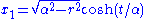
for de Sitter as follows:where
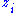gives the standard embedding the (n−2)-sphere in Rn−1. In these coordinates the de Sitter metric takes the form: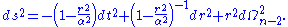Note that there is a cosmological horizon at
.Flat slicing
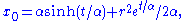
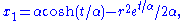
Letwhere
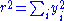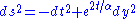
. Then in the coordinates metric reads:where
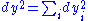is the flat metric on 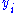's.Open slicing
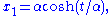
Letwhere
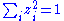forming a 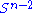with the standard metric . Then the metric of the de Sitter space readswhere
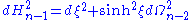
is the metric of a Euclidean hyperbolic space.
Closed slicing
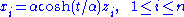
Letwhere
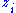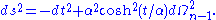
s describe a . Then the metric reads:Changing the time variable to the conformal time via
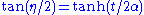(or equivalently ) we obtain a metric conformally equivalent to Einstein static universe: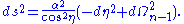This serves to find the Penrose diagram
Penrose diagram
In theoretical physics, a Penrose diagram is a two-dimensional diagram that captures the causal relations between different points in spacetime...
of de Sitter space.
dS slicing
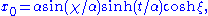
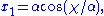
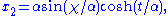
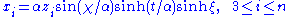
Letwhere
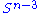s describe a . Then the metric reads: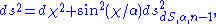where
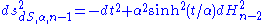
is the metric of an
dimensional de Sitter space with radius of curvature in open slicing coordinates. The hyperbolic metric is given by:This is the analytic continuation of the open slicing coordinates under
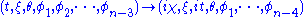and also switching 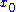and 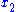because they change their timelike/spacelike nature.See also
- Anti de Sitter spaceAnti de Sitter spaceIn mathematics and physics, n-dimensional anti de Sitter space, sometimes written AdS_n, is a maximally symmetric Lorentzian manifold with constant negative scalar curvature...
- de Sitter universeDe Sitter universeA de Sitter universe is a cosmological solution to Einstein's field equations of General Relativity which is named after Willem de Sitter. It models the universe as spatially flat and neglects ordinary matter, so the dynamics of the universe are dominated by the cosmological constant, thought to...
- AdS/CFT correspondenceAdS/CFT correspondenceIn physics, the AdS/CFT correspondence , sometimes called the Maldacena duality, is the conjectured equivalence between a string theory and gravity defined on one space, and a quantum field theory without gravity defined on the conformal boundary of this space, whose dimension is lower by one or more...
- Hyperboloid
- De Sitter–Schwarzschild metric