Gibbs-Duhem equation
Encyclopedia
In thermodynamics
, the Gibbs–Duhem equation describes the relationship between changes in chemical potential
for components in a thermodynamical system :
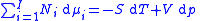
where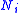
is the number of moles
of component
, 
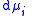the incremental increase in chemical potential
for this component,
the entropy
,
the absolute temperature, 
volume
and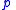
the pressure
. It shows that in thermodynamics intensive properties are not independent but related, making it a mathematical statement of the state postulate
. When pressure and temperature are variable, only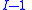
of 
components have independent values for chemical potential and Gibbs' phase rule
follows. The law is named after Josiah Gibbs and Pierre Duhem
.
in terms of its natural variables is
.
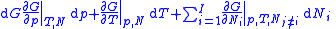With the substitution of two of the Maxwell relations
and the definition of chemical potential
, this is transformed into:
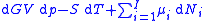
As shown in the Gibbs free energy
article, the chemical potential is just another name for the partial molar (or just partial, depending on the units of N) Gibbs free energy, thus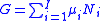
.
The total differential of this expression is
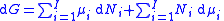
Subtracting the two expressions for the total differential of the Gibbs free energy gives the Gibbs–Duhem relation:
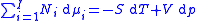
different components, there will be 
independent parameters or "degrees of freedom". For example, if we know a gas cylinder filled with pure nitrogen is at room temperature (298 K) and 25 MPa, we can determine the fluid density (258 kg/m3), enthalpy (272 kJ/kg), entropy (5.07 kJ/kg-K) or any other intensive thermodynamic variable. If instead the cylinder contains a nitrogen/oxygen mixture, we require an additional piece of information, usually the ratio of oxygen-to-nitrogen.
If multiple phases of matter are present, the chemical potentials across a phase boundary are equal. Combining expressions for the Gibbs–Duhem equation in each phase and assuming systematic equilibrium (i.e. that the temperature and pressure is constant throughout the system), we recover the Gibbs' phase rule
.
One particularly useful expression arises when considering binary solutions. At constant P (isobaric
) and T (isothermal) it becomes:
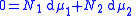
or, normalizing by total number of moles in the system
, substituting in the definition of activity coefficient
and using the identity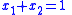 
:
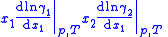
This equation is instrumental in the calculation of thermodynamically consistent and thus more accurate expressions for the vapor pressure
of a fluid mixture from limited experimental data.
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, the Gibbs–Duhem equation describes the relationship between changes in chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
for components in a thermodynamical system :
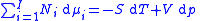
where
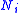is the number of molesMole (unit)
The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
of component
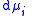, the incremental increase in chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
for this component,
the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
,
the absolute temperature, volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
and
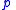the pressurePressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
. It shows that in thermodynamics intensive properties are not independent but related, making it a mathematical statement of the state postulate
Thermodynamic state
A thermodynamic state is a set of values of properties of a thermodynamic system that must be specified to reproduce the system. The individual parameters are known as state variables, state parameters or thermodynamic variables. Once a sufficient set of thermodynamic variables have been...
. When pressure and temperature are variable, only
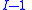of components have independent values for chemical potential and Gibbs' phase ruleGibbs' phase rule
Gibbs' phase rule was proposed by Josiah Willard Gibbs in the 1870s as the equalityF\;=\;C\;-\;P\;+\;2where P is the number of phases in thermodynamic equilibrium with each other and C is the number of components. Typical phases are solids, liquids and gases. A system involving one pure chemical...
follows. The law is named after Josiah Gibbs and Pierre Duhem
Pierre Duhem
Pierre Maurice Marie Duhem was a French physicist, mathematician and philosopher of science, best known for his writings on the indeterminacy of experimental criteria and on scientific development in the Middle Ages...
.
Derivation
Deriving the Gibbs–Duhem equation from basic thermodynamic state equations is straightforward. The total differential of the Gibbs free energyGibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
in terms of its natural variables is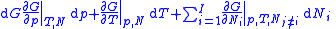.With the substitution of two of the Maxwell relations
Maxwell relations
Maxwell's relations are a set of equations in thermodynamics which are derivable from the definitions of the thermodynamic potentials. The Maxwell relations are statements of equality among the second derivatives of the thermodynamic potentials. They follow directly from the fact that the order of...
and the definition of chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
, this is transformed into:
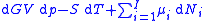
As shown in the Gibbs free energy
Gibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
article, the chemical potential is just another name for the partial molar (or just partial, depending on the units of N) Gibbs free energy, thus
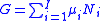.The total differential of this expression is
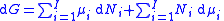
Subtracting the two expressions for the total differential of the Gibbs free energy gives the Gibbs–Duhem relation:
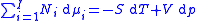
Applications
By normalizing the above equation by the extent of a system, such as the total number of moles, the Gibbs–Duhem equation provides a relationship between the intensive variables of the system. For a simple system with different components, there will be independent parameters or "degrees of freedom". For example, if we know a gas cylinder filled with pure nitrogen is at room temperature (298 K) and 25 MPa, we can determine the fluid density (258 kg/m3), enthalpy (272 kJ/kg), entropy (5.07 kJ/kg-K) or any other intensive thermodynamic variable. If instead the cylinder contains a nitrogen/oxygen mixture, we require an additional piece of information, usually the ratio of oxygen-to-nitrogen.If multiple phases of matter are present, the chemical potentials across a phase boundary are equal. Combining expressions for the Gibbs–Duhem equation in each phase and assuming systematic equilibrium (i.e. that the temperature and pressure is constant throughout the system), we recover the Gibbs' phase rule
Gibbs' phase rule
Gibbs' phase rule was proposed by Josiah Willard Gibbs in the 1870s as the equalityF\;=\;C\;-\;P\;+\;2where P is the number of phases in thermodynamic equilibrium with each other and C is the number of components. Typical phases are solids, liquids and gases. A system involving one pure chemical...
.
One particularly useful expression arises when considering binary solutions. At constant P (isobaric
Isobaric
Isobaric may refer to:*in thermodynamics, an isobaric process, i.e. one that is carried out at constant pressure;...
) and T (isothermal) it becomes:
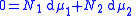
or, normalizing by total number of moles in the system
, substituting in the definition of activity coefficientActivity coefficient
An activity coefficient is a factor used in thermodynamics to account for deviations from ideal behaviour in a mixture of chemical substances. In an ideal mixture, the interactions between each pair of chemical species are the same and, as a result, properties of the mixtures can be expressed...
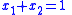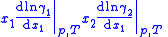
and using the identity :This equation is instrumental in the calculation of thermodynamically consistent and thus more accurate expressions for the vapor pressure
Vapor pressure
Vapor pressure or equilibrium vapor pressure is the pressure of a vapor in thermodynamic equilibrium with its condensed phases in a closed system. All liquids have a tendency to evaporate, and some solids can sublimate into a gaseous form...
of a fluid mixture from limited experimental data.