
Gibbs algorithm
Encyclopedia
In statistical mechanics
, the Gibbs algorithm, first introduced by J. Willard Gibbs in 1878, is the injunction to choose a statistical ensemble (probability distribution) for the unknown microscopic state
of a thermodynamic system
by minimising the average log probability
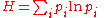
subject to the probability distribution satisfying a set of constraints (usually expectation values) corresponding to the known macroscopic
quantities. Physicists call the result of applying the Gibbs algorithm the Gibbs distribution for the given constraints, most notably Gibbs's grand canonical ensemble
for open systems when the average energy and the average number of particles are given. (See also partition function
).
In the light of Claude Shannon's information theory
, in 1957 E.T. Jaynes re-interpreted the Gibbs algorithm as a much more general, more widely applicable inference technique, leading to the principle of maximum entropy
, and the MaxEnt view of thermodynamics
.
This general result of the Gibbs algorithm is then a maximum entropy probability distribution
. Statisticians identify such distributions as belonging to exponential families
.
iterations, a special case of the Metropolis-Hastings algorithm
.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the Gibbs algorithm, first introduced by J. Willard Gibbs in 1878, is the injunction to choose a statistical ensemble (probability distribution) for the unknown microscopic state
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
of a thermodynamic system
Thermodynamic system
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics....
by minimising the average log probability
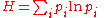
subject to the probability distribution satisfying a set of constraints (usually expectation values) corresponding to the known macroscopic
Macroscopic
The macroscopic scale is the length scale on which objects or processes are of a size which is measurable and observable by the naked eye.When applied to phenomena and abstract objects, the macroscopic scale describes existence in the world as we perceive it, often in contrast to experiences or...
quantities. Physicists call the result of applying the Gibbs algorithm the Gibbs distribution for the given constraints, most notably Gibbs's grand canonical ensemble
Grand canonical ensemble
In statistical mechanics, a grand canonical ensemble is a theoretical collection of model systems put together to mirror the calculated probability distribution of microscopic states of a given physical system which is being maintained in a given macroscopic state...
for open systems when the average energy and the average number of particles are given. (See also partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
).
In the light of Claude Shannon's information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, in 1957 E.T. Jaynes re-interpreted the Gibbs algorithm as a much more general, more widely applicable inference technique, leading to the principle of maximum entropy
Principle of maximum entropy
In Bayesian probability, the principle of maximum entropy is a postulate which states that, subject to known constraints , the probability distribution which best represents the current state of knowledge is the one with largest entropy.Let some testable information about a probability distribution...
, and the MaxEnt view of thermodynamics
Maximum entropy thermodynamics
In physics, maximum entropy thermodynamics views equilibrium thermodynamics and statistical mechanics as inference processes. More specifically, MaxEnt applies inference techniques rooted in Shannon information theory, Bayesian probability, and the principle of maximum entropy...
.
This general result of the Gibbs algorithm is then a maximum entropy probability distribution
Maximum entropy probability distribution
In statistics and information theory, a maximum entropy probability distribution is a probability distribution whose entropy is at least as great as that of all other members of a specified class of distributions....
. Statisticians identify such distributions as belonging to exponential families
Exponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
.
Not to be confused with
The Gibbs sampler, an update algorithm used in Markov chain Monte CarloMarkov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
iterations, a special case of the Metropolis-Hastings algorithm
Metropolis-Hastings algorithm
In mathematics and physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo method for obtaining a sequence of random samples from a probability distribution for which direct sampling is difficult...
.

