Gorman polar form
Encyclopedia
Gorman polar form is a functional form
for indirect utility function
s in economics
. Imposing this form on utility
allows the researcher to treat a society of utility-maximizers as if it consisted of a single 'representative' individual
. W. M. Gorman
showed that having the function
take Gorman polar form is both a necessary and sufficient for this condition to hold.
s should be parallel straight lines. Gorman's first published paper in 1953 developed these ideas in order to answer the question of generalizing a society to a single individual.
In 1961, Gorman published a short, four-page paper in Metroeconomica which derived an explicit expression for the functional form of preferences which give rise to linear Engel curves. Briefly, an individual's (
) resulting expenditure function (
) must be affine
with respect to utility (
):
,
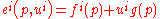where both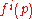
and 
are homogeneous
of degree one in prices (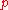
, a vector). This homogeneity condition is trivial, as otherwise 
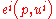would not give linear Engel curves.
and 
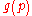have nice interpretations: 
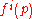is the expenditure needed to reach a reference utility level of zero for each individual (
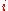), while 
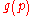is the price index which deflates the excess money income 
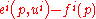needed to attain a level of utility 
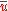. It is important to note that 
is the same for every individual in a society.
,
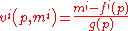where
is the amount of income available to the individual and is equivalent to the expenditure (
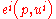) in the previous equation. This is what Gorman called “the polar form of the underlying utility function.” Gorman's use of the term polar was in reference to the idea that the indirect utility function can be seen as using polar rather than Cartesian (as in direct utility functions) coordinates to describe the indifference curve. Here, income (
) is analogous to the radius and prices (
) to an angle.
s of a function in Gorman polar form are linear
, apply Roy's identity
to the utility function to get a Marshallian demand function
for an individual (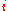
) and a good (
):
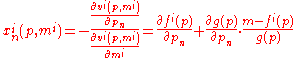
This is linear in income (
), so the change in an individual's demand for some commodity with respect to a change in that individual's income,
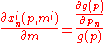, does not depend on income, and thus Engel curves are linear.
Also, since this change does not depend on variables
particular to any individual, the slopes of the Engel curves of different individuals are equal.
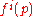and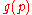 
in certain cases. But the most important application is for the theorist of economics, in that it allows a researcher to treat a society of utility-maximizing individuals as a single individual. In other words, under these conditions a community indifference mapping
is guaranteed to exist.
Functional form
In programming and mathematics, a functional form is an operator or function that can either be applied to other operators or yield operators as result, or both...
for indirect utility function
Indirect utility function
In economics, a consumer's indirect utility functionv gives the consumer's maximal utility when faced with a price level p and an amount of income w. It represents the consumer's preferences over market conditions....
s in economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
. Imposing this form on utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
allows the researcher to treat a society of utility-maximizers as if it consisted of a single 'representative' individual
Representative agent
Economists use the term representative agent to refer to the typical decision-maker of a certain type ....
. W. M. Gorman
W. M. Gorman
William Moore "Terence" Gorman was an Irish economist and academic. He was predominantly a theorist and is most famous for his work on aggregation and separability of goods, and in this context he developed his famous Gorman polar form...
showed that having the function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
take Gorman polar form is both a necessary and sufficient for this condition to hold.
Motivation
Early results by Antonelli (1886) and Nataf (1953) had shown that, assuming all individuals face the same prices in a market, their income consumption curves and their Engel curveEngel curve
An Engel curve describes how household expenditure on a particular good orservice varies with household income. There are two varieties of Engel Curves. Budget share Engel Curves describe how the proportion of household income spent on a good varies with income. Alternatively, Engel curves can also...
s should be parallel straight lines. Gorman's first published paper in 1953 developed these ideas in order to answer the question of generalizing a society to a single individual.
In 1961, Gorman published a short, four-page paper in Metroeconomica which derived an explicit expression for the functional form of preferences which give rise to linear Engel curves. Briefly, an individual's (
) resulting expenditure function () must be affineAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
with respect to utility (
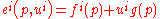):,where both
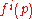and are homogeneousHomogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
of degree one in prices (
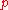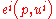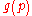, a vector). This homogeneity condition is trivial, as otherwise would not give linear Engel curves. and have nice interpretations: 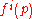is the expenditure needed to reach a reference utility level of zero for each individual (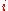), while 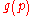is the price index which deflates the excess money income 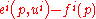needed to attain a level of utility 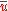. It is important to note that is the same for every individual in a society.Definition
Inverting this formula gives the indirect utility functionIndirect utility function
In economics, a consumer's indirect utility functionv gives the consumer's maximal utility when faced with a price level p and an amount of income w. It represents the consumer's preferences over market conditions....
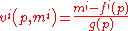,where
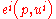is the amount of income available to the individual and is equivalent to the expenditure () in the previous equation. This is what Gorman called “the polar form of the underlying utility function.” Gorman's use of the term polar was in reference to the idea that the indirect utility function can be seen as using polar rather than Cartesian (as in direct utility functions) coordinates to describe the indifference curve. Here, income () is analogous to the radius and prices () to an angle.Proof of linearity and equality of slope of Engel curves
To prove that the Engel curveEngel curve
An Engel curve describes how household expenditure on a particular good orservice varies with household income. There are two varieties of Engel Curves. Budget share Engel Curves describe how the proportion of household income spent on a good varies with income. Alternatively, Engel curves can also...
s of a function in Gorman polar form are linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, apply Roy's identity
Roy's identity
Roy's identity is a major result in microeconomics having applications in consumer choice and the theory of the firm. The lemma relates the ordinary demand function to the derivatives of the indirect utility function...
to the utility function to get a Marshallian demand function
Marshallian demand function
In microeconomics, a consumer's Marshallian demand function specifies what the consumer would buy in each price and wealth situation, assuming it perfectly solves the utility maximization problem...
for an individual (
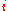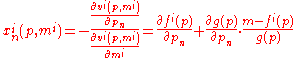
) and a good ():This is linear in income (
), so the change in an individual's demand for some commodity with respect to a change in that individual's income,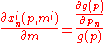, does not depend on income, and thus Engel curves are linear.Also, since this change does not depend on variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
particular to any individual, the slopes of the Engel curves of different individuals are equal.
Application
Many applications of Gorman polar form are summarized in various texts and in Honohan and Neary's article cited at the end of this article. These applications include the ease of estimation of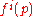 and 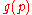in certain cases. But the most important application is for the theorist of economics, in that it allows a researcher to treat a society of utility-maximizing individuals as a single individual. In other words, under these conditions a community indifference mappingIndifference curve
In microeconomic theory, an indifference curve is a graph showing different bundles of goods between which a consumer is indifferent. That is, at each point on the curve, the consumer has no preference for one bundle over another. One can equivalently refer to each point on the indifference curve...
is guaranteed to exist.