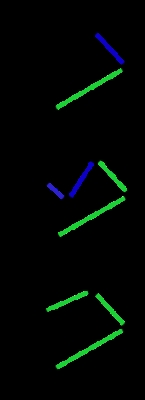
Graham scan
Encyclopedia
The Graham scan is a method of computing the convex hull
of a finite set of points in the plane with time complexity
O
(n log n). It is named after Ronald Graham
, who published the original algorithm in 1972. The algorithm finds all vertices of the convex hull ordered along its boundary.
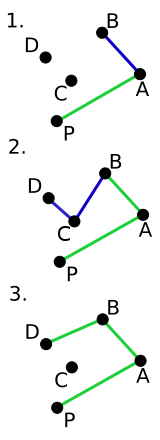The first step in this algorithm is to find the point with the lowest y-coordinate. If the lowest y-coordinate exists in more than one point in the set, the point with the lowest x-coordinate out of the candidates should be chosen. Call this point P. This step takes O
(n), where n is the number of points in question.
Next, the set of points must be sorted in increasing order of the angle they and the point P make with the x-axis. Any general-purpose sorting algorithm
is appropriate for this, for example heapsort
(which is O(n log n)). In order to speed up the calculations, it is not necessary to calculate the actual angle these points make with the x-axis; instead, it suffices to calculate the cosine of this angle: it is a monotonically decreasing function
in the domain in question (which is 0 to 180 degrees, due to the first step) and may be calculated with simple arithmetic.
The algorithm proceeds by considering each of the points in the sorted array in sequence. For each point, it is determined whether moving from the two previously considered points to this point is a "left turn" or a "right turn". If it is a "right turn", this means that the second-to-last point is not part of the convex hull and should be removed from consideration. This process is continued for as long as the set of the last three points is a "right turn". As soon as a "left turn" is encountered, the algorithm moves on to the next point in the sorted array. (If at any stage the three points are collinear, one may opt either to discard or to report it, since in some applications it is required to find all points on the boundary of the convex hull.)
Again, determining whether three points constitute a "left turn" or a "right turn" does not require computing the actual angle between the two line segments, and can actually be achieved with simple arithmetic only. For three points
, 
and 
, simply compute the direction of the cross product
of the two vectors defined by points
, 
and 
, 
, characterized by the sign of the expression 
. If the result is 0, the points are collinear; if it is positive, the three points constitute a "left turn", otherwise a "right turn".
This process will eventually return to the point at which it started, at which point the algorithm is completed and the stack now contains the points on the convex hull in counterclockwise order.
While it may seem that the time complexity of the loop is O(n2), because for each point it goes back to check if any of the previous points make a "right turn", it is actually O(n), because each point is considered at most twice in some sense.
Each point can appear only once as a point
in a "left turn" (because the algorithm advances to the next point 
after that),
and as a point
in a "right turn" (because the point 
is removed). The overall time complexity is therefore O(n log n), since the time to sort dominates the time to actually compute the convex hull.
# Three points are a counter-clockwise turn if ccw > 0, clockwise if
# ccw < 0, and collinear if ccw = 0 because ccw is a determinant that
# gives the signed area of the triangle formed by p1, p2 and p3.
function ccw(p1, p2, p3):
return (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x)
Then let the result be stored in the array
let N = number of points
let points[N+1] = the array of points
swap points[1] with the point with the lowest y-coordinate
sort points by polar angle with points[1]
# We want points[0] to be a sentinel point that will stop the loop.
let points[0] = points[N]
# M will denote the number of points on the convex hull.
let M = 2
for i = 3 to N:
# Find next valid point on convex hull.
while ccw(points[M-1], points[M], points[i]) <= 0:
# Check if first points are collinear, if so ignore unnecessary points.
if M is 2:
swap points[M] with points[i]
i += 1
else
M -= 1
# Update M and swap points[i] to the correct place.
M += 1
swap points[M] with points[i]
This pseudocode is adapted from Sedgewick
and Wayne's Algorithms, 4th edition.
The check in the while statement is necessary to avoid duplicate points on the hull, for example consider the set (0,0); (1,1); (2,2); (0,2). The point (1,1) is not part of the hull because it is collinear to the line passing through (0,0) and (2,2).
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of a finite set of points in the plane with time complexity
Time complexity
In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n log n). It is named after Ronald Graham
Ronald Graham
Ronald Lewis Graham is a mathematician credited by the American Mathematical Society as being "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years"...
, who published the original algorithm in 1972. The algorithm finds all vertices of the convex hull ordered along its boundary.
Algorithm
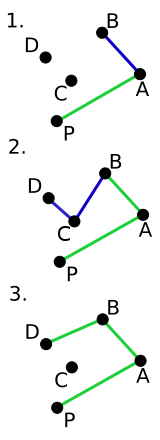
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n), where n is the number of points in question.
Next, the set of points must be sorted in increasing order of the angle they and the point P make with the x-axis. Any general-purpose sorting algorithm
Sorting algorithm
In computer science, a sorting algorithm is an algorithm that puts elements of a list in a certain order. The most-used orders are numerical order and lexicographical order...
is appropriate for this, for example heapsort
Heapsort
Heapsort is a comparison-based sorting algorithm to create a sorted array , and is part of the selection sort family. Although somewhat slower in practice on most machines than a well implemented quicksort, it has the advantage of a more favorable worst-case O runtime...
(which is O(n log n)). In order to speed up the calculations, it is not necessary to calculate the actual angle these points make with the x-axis; instead, it suffices to calculate the cosine of this angle: it is a monotonically decreasing function
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
in the domain in question (which is 0 to 180 degrees, due to the first step) and may be calculated with simple arithmetic.
The algorithm proceeds by considering each of the points in the sorted array in sequence. For each point, it is determined whether moving from the two previously considered points to this point is a "left turn" or a "right turn". If it is a "right turn", this means that the second-to-last point is not part of the convex hull and should be removed from consideration. This process is continued for as long as the set of the last three points is a "right turn". As soon as a "left turn" is encountered, the algorithm moves on to the next point in the sorted array. (If at any stage the three points are collinear, one may opt either to discard or to report it, since in some applications it is required to find all points on the boundary of the convex hull.)
Again, determining whether three points constitute a "left turn" or a "right turn" does not require computing the actual angle between the two line segments, and can actually be achieved with simple arithmetic only. For three points
, and , simply compute the direction of the cross productCross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of the two vectors defined by points
, and , , characterized by the sign of the expression . If the result is 0, the points are collinear; if it is positive, the three points constitute a "left turn", otherwise a "right turn".This process will eventually return to the point at which it started, at which point the algorithm is completed and the stack now contains the points on the convex hull in counterclockwise order.
Time complexity
Sorting the points has time complexity O(n log n).While it may seem that the time complexity of the loop is O(n2), because for each point it goes back to check if any of the previous points make a "right turn", it is actually O(n), because each point is considered at most twice in some sense.
Each point can appear only once as a point
in a "left turn" (because the algorithm advances to the next point after that),and as a point
in a "right turn" (because the point is removed). The overall time complexity is therefore O(n log n), since the time to sort dominates the time to actually compute the convex hull.Pseudocode
First, define# Three points are a counter-clockwise turn if ccw > 0, clockwise if
# ccw < 0, and collinear if ccw = 0 because ccw is a determinant that
# gives the signed area of the triangle formed by p1, p2 and p3.
function ccw(p1, p2, p3):
return (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x)
Then let the result be stored in the array
points.let N = number of points
let points[N+1] = the array of points
swap points[1] with the point with the lowest y-coordinate
sort points by polar angle with points[1]
# We want points[0] to be a sentinel point that will stop the loop.
let points[0] = points[N]
# M will denote the number of points on the convex hull.
let M = 2
for i = 3 to N:
# Find next valid point on convex hull.
while ccw(points[M-1], points[M], points[i]) <= 0:
# Check if first points are collinear, if so ignore unnecessary points.
if M is 2:
swap points[M] with points[i]
i += 1
else
M -= 1
# Update M and swap points[i] to the correct place.
M += 1
swap points[M] with points[i]
This pseudocode is adapted from Sedgewick
Robert Sedgewick (computer scientist)
Robert Sedgewick is a computer science professor at Princeton University and a member of the board of directors of Adobe Systems....
and Wayne's Algorithms, 4th edition.
The check in the while statement is necessary to avoid duplicate points on the hull, for example consider the set (0,0); (1,1); (2,2); (0,2). The point (1,1) is not part of the hull because it is collinear to the line passing through (0,0) and (2,2).