
Sorting algorithm
Encyclopedia
In computer science
, a sorting algorithm is an algorithm
that puts elements of a list in a certain order
. The most-used orders are numerical order and lexicographical order
. Efficient sorting
is important for optimizing the use of other algorithms (such as search
and merge
algorithms) that require sorted lists to work correctly; it is also often useful for canonicalizing
data and for producing human-readable output. More formally, the output must satisfy two conditions:
Since the dawn of computing, the sorting problem has attracted a great deal of research, perhaps due to the complexity of solving it efficiently despite its simple, familiar statement. For example, bubble sort
was analyzed as early as 1956. Although many consider it a solved problem, useful new sorting algorithms are still being invented (for example, library sort
was first published in 2004). Sorting algorithms are prevalent in introductory computer science classes, where the abundance of algorithms for the problem provides a gentle introduction to a variety of core algorithm concepts, such as big O notation
, divide and conquer algorithm
s, data structure
s, randomized algorithm
s, best, worst and average case
analysis, time-space tradeoffs, and lower bounds.
are often classified by:
When equal elements are indistinguishable, such as with integers, or more generally, any data where the entire element is the key, stability is not an issue. However, assume that the following pairs of numbers are to be sorted by their first component:
(4, 2) (3, 7) (3, 1) (5, 6)
In this case, two different results are possible, one which maintains the relative order of records with equal keys, and one which does not:
(3, 7) (3, 1) (4, 2) (5, 6) (order maintained)
(3, 1) (3, 7) (4, 2) (5, 6) (order changed)
Unstable sorting algorithms may change the relative order of records with equal keys, but stable sorting algorithms never do so. Unstable sorting algorithms can be specially implemented to be stable. One way of doing this is to artificially extend the key comparison, so that comparisons between two objects with otherwise equal keys are decided using the order of the entries in the original data order as a tie-breaker. Remembering this order, however, often involves an additional computational cost
.
Sorting based on a primary, secondary, tertiary, etc. sort key can be done by any sorting method, taking all sort keys into account in comparisons (in other words, using a single composite sort key). If a sorting method is stable, it is also possible to sort multiple times, each time with one sort key. In that case the keys need to be applied in order of increasing priority.
Example: sorting pairs of numbers as above by second, then first component:
(4, 2) (3, 7) (3, 1) (5, 6) (original)
(3, 1) (4, 2) (5, 6) (3, 7) (after sorting by second component)
(3, 1) (3, 7) (4, 2) (5, 6) (after sorting by first component)
On the other hand:
(3, 7) (3, 1) (4, 2) (5, 6) (after sorting by first component)
(3, 1) (4, 2) (5, 6) (3, 7) (after sorting by second component,
order by first component is disrupted).
s. The run time and the memory of algorithms could be measured using various notations like theta, sigma, Big-O, small-o, etc. The memory and the run times below are applicable for all the 5 notations.
The following table describes integer sorting
algorithms and other sorting algorithms that are not comparison sort
s. As such, they are not limited by a lower bound. Complexities below are in terms of n, the number of items to be sorted, k, the size of each key, and d, the digit size used by the implementation. Many of them are based on the assumption that the key size is large enough that all entries have unique key values, and hence that n << 2k, where << means "much less than."
lower bound. Complexities below are in terms of n, the number of items to be sorted, k, the size of each key, and d, the digit size used by the implementation. Many of them are based on the assumption that the key size is large enough that all entries have unique key values, and hence that n << 2k, where << means "much less than."
The following table describes some sorting algorithms that are impractical for real-life use due to extremely poor performance or a requirement for specialized hardware.
Additionally, theoretical computer scientists have detailed other sorting algorithms that provide better than time complexity with additional constraints, including:
time complexity with additional constraints, including:
Algorithms not yet compared above include:
Bubble sort average case and worst case are both O(n²).
comparison sort
. It has O
(n2) complexity, making it inefficient on large lists, and generally performs worse than the similar insertion sort
. Selection sort is noted for its simplicity, and also has performance advantages over more complicated algorithms in certain situations.
The algorithm finds the minimum value, swaps it with the value in the first position, and repeats these steps for the remainder of the list. It does no more than n swaps, and thus is useful where swapping is very expensive.
(see below) is a variant of insertion sort that is more efficient for larger lists.
in 1959. It improves upon bubble sort and insertion sort by moving out of order elements more than one position at a time. One implementation can be described as arranging the data sequence in a two-dimensional array and then sorting the columns of the array using insertion sort.
, and rivals algorithms like Quicksort. The basic idea is to eliminate turtles, or small values near the end of the list, since in a bubble sort these slow the sorting down tremendously. (Rabbits, large values around the beginning of the list, do not pose a problem in bubble sort.)
, Python
(as timsort
), and Java
(also uses timsort as of JDK7), among others. Merge sort has been used in Java at least since 2000 in JDK1.3.
. It also works by determining the largest (or smallest) element of the list, placing that at the end (or beginning) of the list, then continuing with the rest of the list, but accomplishes this task efficiently by using a data structure called a heap
, a special type of binary tree
. Once the data list has been made into a heap, the root node is guaranteed to be the largest (or smallest) element. When it is removed and placed at the end of the list, the heap is rearranged so the largest element remaining moves to the root. Using the heap, finding the next largest element takes O(log n) time, instead of O(n) for a linear scan as in simple selection sort. This allows Heapsort to run in O(n log n) time, and this is also the worst case complexity.
algorithm
which relies on a partition operation: to partition an array an element called a pivot is selected. All elements smaller than the pivot are moved before it and all greater elements are moved after it. This can be done efficiently in linear time and in-place
. The lesser and greater sublists are then recursively sorted. Efficient implementations of quicksort (with in-place partitioning) are typically unstable sorts and somewhat complex, but are among the fastest sorting algorithms in practice. Together with its modest O(log n) space usage, quicksort is one of the most popular sorting algorithms and is available in many standard programming libraries. The most complex issue in quicksort is choosing a good pivot element; consistently poor choices of pivots can result in drastically slower O(n²) performance, if at each step the median
is chosen as the pivot then the algorithm works in O(n log n). Finding the median however, is an O(n) operation on unsorted lists and therefore exacts its own penalty with sorting.
sorting algorithm that generalizes Counting sort
by partitioning an array into a finite number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. A variation of this method called the single buffered count sort is faster than quicksort.
Due to the fact that bucket sort must use a limited number of buckets it is best suited to be used on data sets of a limited scope. Bucket sort would be unsuitable for data such as social security numbers - which have a lot of variation.
algorithm to be used internally by the radix sort. Hybrid sorting approach, such as using insertion sort
for small bins improves performance of radix sort significantly.
, Flashsort
.
speed (or, with caching, even at CPU
speed), which, compared to disk speed, is virtually instantaneous.
For example, the popular recursive quicksort algorithm provides quite reasonable performance with adequate RAM, but due to the recursive way that it copies portions of the array it becomes much less practical when the array does not fit in RAM, because it may cause a number of slow copy or move operations to and from disk. In that scenario, another algorithm may be preferable even if it requires more total comparisons.
One way to work around this problem, which works well when complex records (such as in a relational database
) are being sorted by a relatively small key field, is to create an index into the array and then sort the index, rather than the entire array. (A sorted version of the entire array can then be produced with one pass, reading from the index, but often even that is unnecessary, as having the sorted index is adequate.) Because the index is much smaller than the entire array, it may fit easily in memory where the entire array would not, effectively eliminating the disk-swapping problem. This procedure is sometimes called "tag sort".
Another technique for overcoming the memory-size problem is to combine two algorithms in a way that takes advantages of the strength of each to improve overall performance. For instance, the array might be subdivided into chunks of a size that will fit easily in RAM (say, a few thousand elements), the chunks sorted using an efficient algorithm (such as quicksort or heapsort
), and the results merged as per mergesort. This is less efficient than just doing mergesort in the first place, but it requires less physical RAM (to be practical) than a full quicksort on the whole array.
Techniques can also be combined. For sorting very large sets of data that vastly exceed system memory, even the index may need to be sorted using an algorithm or combination of algorithms designed to perform reasonably with virtual memory
, i.e., to reduce the amount of swapping required.
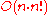 , Stooge sort
, Stooge sort
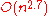 .
.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a sorting algorithm is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that puts elements of a list in a certain order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
. The most-used orders are numerical order and lexicographical order
Lexicographical order
In mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
. Efficient sorting
Sorting
Sorting is any process of arranging items in some sequence and/or in different sets, and accordingly, it has two common, yet distinct meanings:# ordering: arranging items of the same kind, class, nature, etc...
is important for optimizing the use of other algorithms (such as search
Search algorithm
In computer science, a search algorithm is an algorithm for finding an item with specified properties among a collection of items. The items may be stored individually as records in a database; or may be elements of a search space defined by a mathematical formula or procedure, such as the roots...
and merge
Merge algorithm
Merge algorithms are a family of algorithms that run sequentially over multiple sorted lists, typically producing more sorted lists as output. This is well-suited for machines with tape drives...
algorithms) that require sorted lists to work correctly; it is also often useful for canonicalizing
Canonicalization
In computer science, canonicalization , is a process for converting data that has more than one possible representation into a "standard", "normal", or canonical form...
data and for producing human-readable output. More formally, the output must satisfy two conditions:
- The output is in nondecreasing order (each element is no smaller than the previous element according to the desired total orderTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
); - The output is a permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
, or reordering, of the input.
Since the dawn of computing, the sorting problem has attracted a great deal of research, perhaps due to the complexity of solving it efficiently despite its simple, familiar statement. For example, bubble sort
Bubble sort
Bubble sort, also known as sinking sort, is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which...
was analyzed as early as 1956. Although many consider it a solved problem, useful new sorting algorithms are still being invented (for example, library sort
Library sort
Library sort, or gapped insertion sort is a sorting algorithm that uses an insertion sort, but with gaps in the array to accelerate subsequent insertions...
was first published in 2004). Sorting algorithms are prevalent in introductory computer science classes, where the abundance of algorithms for the problem provides a gentle introduction to a variety of core algorithm concepts, such as big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, divide and conquer algorithm
Divide and conquer algorithm
In computer science, divide and conquer is an important algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same type, until these become simple enough to be solved directly...
s, data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
s, randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
s, best, worst and average case
Best, worst and average case
In computer science, best, worst and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively...
analysis, time-space tradeoffs, and lower bounds.
Classification
Sorting algorithms used in computer scienceComputer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
are often classified by:
- Computational complexityComputational complexity theoryComputational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
(worst, average and best behaviour) of element comparisons in terms of the size of the list . For typical sorting algorithms good behavior is
. For typical sorting algorithms good behavior is  Big O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
Big O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or... and bad behavior is
and bad behavior is 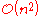 . (See Big O notationBig O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
. (See Big O notationBig O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
.) Ideal behavior for a sort is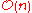 , but this is not possible in the average case. Comparison-based sorting algorithmsComparison sortA comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list...
, but this is not possible in the average case. Comparison-based sorting algorithmsComparison sortA comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list...
, which evaluate the elements of the list via an abstract key comparison operation, need at least comparisons for most inputs.
comparisons for most inputs. - Computational complexityComputational complexity theoryComputational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
of swaps (for "in place" algorithms). - Memory usage (and use of other computer resources). In particular, some sorting algorithms are "in placeIn-place algorithmIn computer science, an in-place algorithm is an algorithm which transforms input using a data structure with a small, constant amount of extra storage space. The input is usually overwritten by the output as the algorithm executes...
". This means that they need only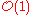 or
or 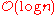 memory beyond the items being sorted and they don't need to create auxiliary locations for data to be temporarily stored, as in other sorting algorithms.
memory beyond the items being sorted and they don't need to create auxiliary locations for data to be temporarily stored, as in other sorting algorithms. - Recursion. Some algorithms are either recursive or non-recursive, while others may be both (e.g., merge sort).
- Stability: stable sorting algorithms maintain the relative order of records with equal keys (i.e., values).
- Whether or not they are a comparison sortComparison sortA comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list...
. A comparison sort examines the data only by comparing two elements with a comparison operator. - General method: insertion, exchange, selection, merging, etc.. Exchange sorts include bubble sort and quicksort. Selection sorts include shaker sort and heapsort.
- Adaptability: Whether or not the presortedness of the input affects the running time. Algorithms that take this into account are known to be adaptiveAdaptive sortA sorting algorithm falls into the adaptive sort family if it takes advantage of existing order in its input. It benefits from the presortedness in the input sequence – or a limited amount of disorder for various definitions of measures of disorder – and sorts faster...
.
Stability
Stable sorting algorithms maintain the relative order of records with equal keys. If all keys are different then this distinction is not necessary. But if there are equal keys, then a sorting algorithm is stable if whenever there are two records (let's say R and S) with the same key, and R appears before S in the original list, then R will always appear before S in the sorted list.When equal elements are indistinguishable, such as with integers, or more generally, any data where the entire element is the key, stability is not an issue. However, assume that the following pairs of numbers are to be sorted by their first component:
(4, 2) (3, 7) (3, 1) (5, 6)
In this case, two different results are possible, one which maintains the relative order of records with equal keys, and one which does not:
(3, 7) (3, 1) (4, 2) (5, 6) (order maintained)
(3, 1) (3, 7) (4, 2) (5, 6) (order changed)
Unstable sorting algorithms may change the relative order of records with equal keys, but stable sorting algorithms never do so. Unstable sorting algorithms can be specially implemented to be stable. One way of doing this is to artificially extend the key comparison, so that comparisons between two objects with otherwise equal keys are decided using the order of the entries in the original data order as a tie-breaker. Remembering this order, however, often involves an additional computational cost
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
.
Sorting based on a primary, secondary, tertiary, etc. sort key can be done by any sorting method, taking all sort keys into account in comparisons (in other words, using a single composite sort key). If a sorting method is stable, it is also possible to sort multiple times, each time with one sort key. In that case the keys need to be applied in order of increasing priority.
Example: sorting pairs of numbers as above by second, then first component:
(4, 2) (3, 7) (3, 1) (5, 6) (original)
(3, 1) (4, 2) (5, 6) (3, 7) (after sorting by second component)
(3, 1) (3, 7) (4, 2) (5, 6) (after sorting by first component)
On the other hand:
(3, 7) (3, 1) (4, 2) (5, 6) (after sorting by first component)
(3, 1) (4, 2) (5, 6) (3, 7) (after sorting by second component,
order by first component is disrupted).
Comparison of algorithms
In this table, n is the number of records to be sorted. The columns "Average" and "Worst" give the time complexity in each case, under the assumption that the length of each key is constant, and that therefore all comparisons, swaps, and other needed operations can proceed in constant time. "Memory" denotes the amount of auxiliary storage needed beyond that used by the list itself, under the same assumption. These are all comparison sortComparison sort
A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list...
s. The run time and the memory of algorithms could be measured using various notations like theta, sigma, Big-O, small-o, etc. The memory and the run times below are applicable for all the 5 notations.
| Name | Best | Average | Worst | Memory | Stable | Method | Quicksort | Depends | Partitioning | Quicksort can be done in place with O(log(n)) stack space, but the sort is unstable. Naïve variants use an O(n) space array to store the partition. An O(n) space implementation can be stable. |
|---|---|---|---|---|---|---|---|
| Merge sort Merge sort Merge sort is an O comparison-based sorting algorithm. Most implementations produce a stable sort, meaning that the implementation preserves the input order of equal elements in the sorted output. It is a divide and conquer algorithm... |
Yes | Merging | Used to sort this table in Firefox http://mxr.mozilla.org/seamonkey/source/js/src/jsarray.c. | ||||
| In-place Merge sort Merge sort Merge sort is an O comparison-based sorting algorithm. Most implementations produce a stable sort, meaning that the implementation preserves the input order of equal elements in the sorted output. It is a divide and conquer algorithm... |
Yes | Merging | Implemented in Standard Template Library (STL): http://www.sgi.com/tech/stl/stable_sort.html; can be implemented as a stable sort based on stable in-place merging: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.54.8381 | ||||
| Heapsort Heapsort Heapsort is a comparison-based sorting algorithm to create a sorted array , and is part of the selection sort family. Although somewhat slower in practice on most machines than a well implemented quicksort, it has the advantage of a more favorable worst-case O runtime... |
No | Selection | |||||
| Insertion sort Insertion sort Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort... |
Yes | Insertion | Average case is also  , where d is the number of inversions , where d is the number of inversions |
||||
| Introsort Introsort Introsort or introspective sort is a sorting algorithm designed by David Musser in 1997. It begins with quicksort and switches to heapsort when the recursion depth exceeds a level based on the number of elements being sorted... |
No | Partitioning & Selection | Used in SGI Silicon Graphics Silicon Graphics, Inc. was a manufacturer of high-performance computing solutions, including computer hardware and software, founded in 1981 by Jim Clark... STL Standard Template Library The Standard Template Library is a C++ software library which later evolved into the C++ Standard Library. It provides four components called algorithms, containers, functors, and iterators. More specifically, the C++ Standard Library is based on the STL published by SGI. Both include some... implementations |
||||
| Selection sort Selection sort Selection sort is a sorting algorithm, specifically an in-place comparison sort. It has O time complexity, making it inefficient on large lists, and generally performs worse than the similar insertion sort... |
Depends http://www.algolist.net/Algorithms/Sorting/Selection_sort. | Selection | Its stability depends on the implementation. Used to sort this table in Safari or other Webkit web browser http://svn.webkit.org/repository/webkit/trunk/Source/JavaScriptCore/runtime/ArrayPrototype.cpp. | ||||
| Timsort Timsort Timsort is a hybrid sorting algorithm, derived from merge sort and insertion sort, designed to perform well on many kinds of real-world data. It was invented by Tim Peters in 2002 for use in the Python programming language. The algorithm is designed to find subsets of the data which are already... |
Yes | Insertion & Merging |  comparisons when the data is already sorted or reverse sorted. comparisons when the data is already sorted or reverse sorted. |
||||
| Shell sort Shell sort Shellsort, also known as Shell sort or Shell's method is an in-place comparison sort. It generalizes an exchanging sort, such as insertion or bubble sort, by allowing the comparison and exchange of elements that lie far apart. Its first version was published by Donald Shell in 1959. The running... |
No | Insertion | |||||
| Bubble sort Bubble sort Bubble sort, also known as sinking sort, is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which... |
Yes | Exchanging | Tiny code size | ||||
| Binary tree sort | Yes | Insertion | When using a self-balancing binary search tree Self-balancing binary search tree In computer science, a self-balancing binary search tree is any node based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions.... |
||||
| Cycle sort Cycle sort Cycle sort is an in-place, unstable sorting algorithm, a comparison sort that is theoretically optimal in terms of the total number of writes to the original array, unlike any other in-place sorting algorithm... |
No | Insertion | In-place with theoretically optimal number of writes | ||||
| Library sort Library sort Library sort, or gapped insertion sort is a sorting algorithm that uses an insertion sort, but with gaps in the array to accelerate subsequent insertions... |
Yes | Insertion | |||||
| Patience sorting Patience sorting Patience sorting is a sorting algorithm, based on a solitaire card game, that has the property of being able to efficiently compute the length of a longest increasing subsequence in a given array.-The card game:... |
No | Insertion & Selection | Finds all the longest increasing subsequence Longest increasing subsequence The longest increasing subsequence problem is to find a subsequence of a given sequence in which the subsequence elements are in sorted order, lowest to highest, and in which the subsequence is as long as possible... s within O(n log n) |
||||
| Smoothsort Smoothsort Smoothsort is a comparison-based sorting algorithm. It is a variation of heapsort developed by Edsger Dijkstra in 1981. Like heapsort, smoothsort's upper bound is O... |
No | Selection | An adaptive sort Adaptive sort A sorting algorithm falls into the adaptive sort family if it takes advantage of existing order in its input. It benefits from the presortedness in the input sequence – or a limited amount of disorder for various definitions of measures of disorder – and sorts faster... -  comparisons when the data is already sorted, and 0 swaps. comparisons when the data is already sorted, and 0 swaps. |
||||
| Strand sort Strand sort Strand sort is a sorting algorithm. It works by repeatedly pulling sorted sublists out of the list to be sorted and merging them with a result array... |
Yes | Selection | |||||
| Tournament sort Tournament sort Tournament sort is a sorting algorithm. It improves upon the naive selection sort by using a priority queue to find the next element in the sort. In the naive selection sort, it takes O operations to select the next element of n elements; in a tournament sort, it takes O operations... |
Selection | ||||||
| Cocktail sort Cocktail sort Cocktail sort, also known as bidirectional bubble sort, cocktail shaker sort, shaker sort , ripple sort, shuffle sort, shuttle sort or happy hour sort, is a variation of bubble sort that is both a stable sorting algorithm and a comparison sort... |
Yes | Exchanging | |||||
| Comb sort Comb sort Comb sort is a relatively simplistic sorting algorithm originally designed by Włodzimierz Dobosiewicz in 1980. Later it was rediscovered and popularized by Stephen Lacey and Richard Box with a Byte Magazine . Comb sort improves on bubble sort, and rivals algorithms like Quicksort... |
No | Exchanging | Small code size | ||||
| Gnome sort Gnome sort Gnome sort, originally proposed by Hamid Sarbazi-Azad in 2000 and called , and then later on described by Dick Grune and named "Gnome sort", is a sorting algorithm which is similar to insertion sort, except that moving an element to its proper place is accomplished by a series of swaps, as in... |
Yes | Exchanging | Tiny code size | ||||
| Bogosort Bogosort In computer science, bogosort is a particularly ineffective sorting algorithm based on the generate and test paradigm. It is not useful for sorting, but may be used for educational purposes, to contrast it with other more realistic algorithms; it has also been used as an example in logic programming... |
No | Luck | Randomly permute the array and check if sorted. |
The following table describes integer sorting
Integer sorting
In computer science, integer sorting is the algorithmic problem of sorting a collection of data values by numeric keys, each of which is an integer. Algorithms designed for integer sorting may also often be applied to sorting problems in which the keys are floating point numbers or text strings...
algorithms and other sorting algorithms that are not comparison sort
Comparison sort
A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list...
s. As such, they are not limited by a
 lower bound. Complexities below are in terms of n, the number of items to be sorted, k, the size of each key, and d, the digit size used by the implementation. Many of them are based on the assumption that the key size is large enough that all entries have unique key values, and hence that n << 2k, where << means "much less than."
lower bound. Complexities below are in terms of n, the number of items to be sorted, k, the size of each key, and d, the digit size used by the implementation. Many of them are based on the assumption that the key size is large enough that all entries have unique key values, and hence that n << 2k, where << means "much less than."| Name | Best | Average | Worst | Memory | Stable | n << 2k | Notes |
|---|---|---|---|---|---|---|---|
| Pigeonhole sort Pigeonhole sort Pigeonhole sorting, also known as count sort , is a sorting algorithm that is suitable for sorting lists of elements where the number of elements and the number of possible key values are approximately the same... |
 |
 |
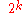 |
Yes | Yes | ||
| Bucket sort Bucket sort Bucket sort, or bin sort, is a sorting algorithm that works by partitioning an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a distribution sort, and is a cousin of... (uniform keys) |
 |
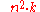 |
 |
Yes | No | Assumes uniform distribution of elements from the domain in the array. | |
| Bucket sort Bucket sort Bucket sort, or bin sort, is a sorting algorithm that works by partitioning an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a distribution sort, and is a cousin of... (integer keys) |
 |
 |
 |
Yes | Yes | r is the range of numbers to be sorted. If r = 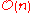 then Avg RT = then Avg RT = 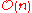 |
|
| Counting sort Counting sort In computer science, counting sort is an algorithm for sorting a collection of objects according to keys that are small integers; that is, it is an integer sorting algorithm. It operates by counting the number of objects that have each distinct key value, and using arithmetic on those counts to... |
 |
 |
 |
Yes | Yes | r is the range of numbers to be sorted. If r = 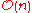 then Avg RT = then Avg RT = 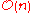 |
|
| LSD Radix Sort | 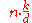 |
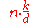 |
 |
Yes | No | ||
| MSD Radix Sort | 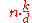 |
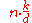 |
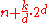 |
Yes | No | Stable version uses an external array of size n to hold all of the bins | |
| MSD Radix Sort | 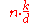 |
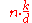 |
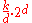 |
No | No | In-Place. k / d recursion levels, 2d for count array | |
| Spreadsort Spreadsort Spreadsort is a sorting algorithm invented by Steven J. Ross in 2002. It combines concepts from distribution-based sorts, such as radix sort and bucket sort, with partitioning concepts from comparison sorts such as quicksort and mergesort... |
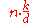 |
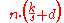 |
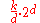 |
No | No | Asymptotics are based on the assumption that n << 2k, but the algorithm does not require this. |
The following table describes some sorting algorithms that are impractical for real-life use due to extremely poor performance or a requirement for specialized hardware.
| Name | Best | Average | Worst | Memory | Stable | Comparison | Other notes |
|---|---|---|---|---|---|---|---|
| Bead sort Bead sort Bead sort is a natural sorting algorithm, developed by Joshua J. Arulanandham, Cristian S. Calude and Michael J. Dinneen in 2002, and published in The Bulletin of the European Association for Theoretical Computer Science... |
N/A | N/A | — | N/A | No | Requires specialized hardware | |
| Simple pancake sort Pancake sorting Pancake sorting is a variation of the sorting problem in which the only allowed operation is to reverse the elements of some prefix of the sequence. Unlike a traditional sorting algorithm, which attempts to sort with the fewest comparisons possible, the goal is to sort the sequence in as few... |
 |
 |
 |
No | Yes | Count is number of flips. | |
| Spaghetti (Poll) sort Spaghetti sort Spaghetti sort is a linear-time, analog algorithm for sorting a sequence of items, introduced by Alexander Dewdney in his Scientific American column.-Algorithm:... |
Yes | Polling | This A linear-time, analog algorithm for sorting a sequence of items, requiring O(n) stack space, and the sort is stable. This requires  parallel processors. Spaghetti sort#Analysis parallel processors. Spaghetti sort#Analysis |
||||
| Sorting network Sorting network A sorting network is an abstract mathematical model of a network of wires and comparator modules that is used to sort a sequence of numbers. Each comparator connects two wires and sorts the values by outputting the smaller value to one wire, and the larger to the other... s |
 |
 |
 |
Yes | No | Requires a custom circuit of size 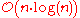 |
Additionally, theoretical computer scientists have detailed other sorting algorithms that provide better than
 time complexity with additional constraints, including:
time complexity with additional constraints, including:- Han's algorithm, a deterministic algorithm for sorting keys from a domain of finite size, taking
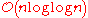 time and
time and 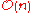 space.
space. - Thorup's algorithm, a randomized algorithm for sorting keys from a domain of finite size, taking
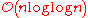 time and
time and 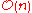 space.
space. - An integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
sorting algorithm taking expected time and
expected time and 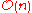 space.
space.
Algorithms not yet compared above include:
- Odd-even sortOdd-even sortIn computing, an odd–even sort or odd–even transposition sort is a relatively simple sorting algorithm, developed originally for use on parallel processors with local interconnections. It is a comparison sort related to bubble sort, with which it shares many characteristics...
- FlashsortFlashsortFlashsort is a distribution sorting algorithm showing linear computational complexity O for uniformly distributed data sets and relatively little additional memory requirement...
- BurstsortBurstsortBurstsort and its variants are cache-efficient algorithms for sorting strings and are faster than quicksort and radix sort for large data sets....
- Postman sort
- Stooge sortStooge sortStooge sort is a recursive sorting algorithm with a time complexity of ).The running time of the algorithm is thus extremely slow comparedto efficient sorting algorithms, such as Merge sort, and is even slower than Bubble sort, a canonical example of a fairly inefficient and simple sort.The...
- SamplesortSamplesortSamplesort is a sorting algorithm described in the 1970 paper "Samplesort: A Sampling Approach to Minimal Storage Tree Sorting", by W D Frazer and A C McKellar....
- Bitonic sorterBitonic sorterBitonic mergesort is a parallel algorithm for sorting. It is also used as a construction method for building a sorting network. The algorithm was devised by Ken Batcher...
- Cocktail sortCocktail sortCocktail sort, also known as bidirectional bubble sort, cocktail shaker sort, shaker sort , ripple sort, shuffle sort, shuttle sort or happy hour sort, is a variation of bubble sort that is both a stable sorting algorithm and a comparison sort...
- Topological sort
Bubble sort
Bubble sort is a simple sorting algorithm. The algorithm starts at the beginning of the data set. It compares the first two elements, and if the first is greater than the second, it swaps them. It continues doing this for each pair of adjacent elements to the end of the data set. It then starts again with the first two elements, repeating until no swaps have occurred on the last pass. This algorithm's average and worst case performance is O(n2), so it is rarely used to sort large, unordered, data sets. Bubble sort can be used to sort a small number of items (where its inefficiency is not a high penalty). Bubble sort may also be efficiently used on a list that is already sorted except for a very small number of elements. For example, if only one element is not in order, bubble sort will take only 2n time. If two elements are not in order, bubble sort will take only at most 3n time.Bubble sort average case and worst case are both O(n²).
Selection sort
Selection sort is an in-placeIn-place algorithm
In computer science, an in-place algorithm is an algorithm which transforms input using a data structure with a small, constant amount of extra storage space. The input is usually overwritten by the output as the algorithm executes...
comparison sort
Comparison sort
A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list...
. It has O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n2) complexity, making it inefficient on large lists, and generally performs worse than the similar insertion sort
Insertion sort
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort...
. Selection sort is noted for its simplicity, and also has performance advantages over more complicated algorithms in certain situations.
The algorithm finds the minimum value, swaps it with the value in the first position, and repeats these steps for the remainder of the list. It does no more than n swaps, and thus is useful where swapping is very expensive.
Insertion sort
Insertion sort is a simple sorting algorithm that is relatively efficient for small lists and mostly sorted lists, and often is used as part of more sophisticated algorithms. It works by taking elements from the list one by one and inserting them in their correct position into a new sorted list. In arrays, the new list and the remaining elements can share the array's space, but insertion is expensive, requiring shifting all following elements over by one. Shell sortShell sort
Shellsort, also known as Shell sort or Shell's method is an in-place comparison sort. It generalizes an exchanging sort, such as insertion or bubble sort, by allowing the comparison and exchange of elements that lie far apart. Its first version was published by Donald Shell in 1959. The running...
(see below) is a variant of insertion sort that is more efficient for larger lists.
Shell sort
Shell sort was invented by Donald ShellDonald Shell
Donald L. Shell is a retired American computer scientist who designed the Shell sort sorting algorithm. He acquired his Ph.D. in Mathematics from the University of Cincinnati in 1959, after publishing the shell sort algorithm in the Communications of the ACM in July the same year.After acquiring...
in 1959. It improves upon bubble sort and insertion sort by moving out of order elements more than one position at a time. One implementation can be described as arranging the data sequence in a two-dimensional array and then sorting the columns of the array using insertion sort.
Comb sort
Comb sort is a relatively simplistic sorting algorithm originally designed by Wlodzimierz Dobosiewicz in 1980. Later it was rediscovered and popularized by Stephen Lacey and Richard Box with a Byte Magazine article published in April 1991. Comb sort improves on bubble sortBubble sort
Bubble sort, also known as sinking sort, is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which...
, and rivals algorithms like Quicksort. The basic idea is to eliminate turtles, or small values near the end of the list, since in a bubble sort these slow the sorting down tremendously. (Rabbits, large values around the beginning of the list, do not pose a problem in bubble sort.)
Merge sort
Merge sort takes advantage of the ease of merging already sorted lists into a new sorted list. It starts by comparing every two elements (i.e., 1 with 2, then 3 with 4...) and swapping them if the first should come after the second. It then merges each of the resulting lists of two into lists of four, then merges those lists of four, and so on; until at last two lists are merged into the final sorted list. Of the algorithms described here, this is the first that scales well to very large lists, because its worst-case running time is O(n log n). Merge sort has seen a relatively recent surge in popularity for practical implementations, being used for the standard sort routine in the programming languages PerlPerl
Perl is a high-level, general-purpose, interpreted, dynamic programming language. Perl was originally developed by Larry Wall in 1987 as a general-purpose Unix scripting language to make report processing easier. Since then, it has undergone many changes and revisions and become widely popular...
, Python
Python (programming language)
Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
(as timsort
Timsort
Timsort is a hybrid sorting algorithm, derived from merge sort and insertion sort, designed to perform well on many kinds of real-world data. It was invented by Tim Peters in 2002 for use in the Python programming language. The algorithm is designed to find subsets of the data which are already...
), and Java
Java (programming language)
Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
(also uses timsort as of JDK7), among others. Merge sort has been used in Java at least since 2000 in JDK1.3.
Heapsort
Heapsort is a much more efficient version of selection sortSelection sort
Selection sort is a sorting algorithm, specifically an in-place comparison sort. It has O time complexity, making it inefficient on large lists, and generally performs worse than the similar insertion sort...
. It also works by determining the largest (or smallest) element of the list, placing that at the end (or beginning) of the list, then continuing with the rest of the list, but accomplishes this task efficiently by using a data structure called a heap
Heap (data structure)
In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: if B is a child node of A, then key ≥ key. This implies that an element with the greatest key is always in the root node, and so such a heap is sometimes called a max-heap...
, a special type of binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
. Once the data list has been made into a heap, the root node is guaranteed to be the largest (or smallest) element. When it is removed and placed at the end of the list, the heap is rearranged so the largest element remaining moves to the root. Using the heap, finding the next largest element takes O(log n) time, instead of O(n) for a linear scan as in simple selection sort. This allows Heapsort to run in O(n log n) time, and this is also the worst case complexity.
Quicksort
Quicksort is a divide and conquerDivide and conquer algorithm
In computer science, divide and conquer is an important algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same type, until these become simple enough to be solved directly...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
which relies on a partition operation: to partition an array an element called a pivot is selected. All elements smaller than the pivot are moved before it and all greater elements are moved after it. This can be done efficiently in linear time and in-place
In-place algorithm
In computer science, an in-place algorithm is an algorithm which transforms input using a data structure with a small, constant amount of extra storage space. The input is usually overwritten by the output as the algorithm executes...
. The lesser and greater sublists are then recursively sorted. Efficient implementations of quicksort (with in-place partitioning) are typically unstable sorts and somewhat complex, but are among the fastest sorting algorithms in practice. Together with its modest O(log n) space usage, quicksort is one of the most popular sorting algorithms and is available in many standard programming libraries. The most complex issue in quicksort is choosing a good pivot element; consistently poor choices of pivots can result in drastically slower O(n²) performance, if at each step the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
is chosen as the pivot then the algorithm works in O(n log n). Finding the median however, is an O(n) operation on unsorted lists and therefore exacts its own penalty with sorting.
Counting sort
Counting sort is applicable when each input is known to belong to a particular set, S, of possibilities. The algorithm runs in O(|S| + n) time and O(|S|) memory where n is the length of the input. It works by creating an integer array of size |S| and using the ith bin to count the occurrences of the ith member of S in the input. Each input is then counted by incrementing the value of its corresponding bin. Afterward, the counting array is looped through to arrange all of the inputs in order. This sorting algorithm cannot often be used because S needs to be reasonably small for it to be efficient, but the algorithm is extremely fast and demonstrates great asymptotic behavior as n increases. It also can be modified to provide stable behavior.Bucket sort
Bucket sort is a divide and conquerDivide and conquer algorithm
In computer science, divide and conquer is an important algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same type, until these become simple enough to be solved directly...
sorting algorithm that generalizes Counting sort
Counting sort
In computer science, counting sort is an algorithm for sorting a collection of objects according to keys that are small integers; that is, it is an integer sorting algorithm. It operates by counting the number of objects that have each distinct key value, and using arithmetic on those counts to...
by partitioning an array into a finite number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. A variation of this method called the single buffered count sort is faster than quicksort.
Due to the fact that bucket sort must use a limited number of buckets it is best suited to be used on data sets of a limited scope. Bucket sort would be unsuitable for data such as social security numbers - which have a lot of variation.
Radix sort
Radix sort is an algorithm that sorts numbers by processing individual digits. n numbers consisting of k digits each are sorted in O(n · k) time. Radix sort can process digits of each number either starting from the least significant digit (LSD) or starting from the most significant digit (MSD). The LSD algorithm first sorts the list by the least significant digit while preserving their relative order using a stable sort. Then it sorts them by the next digit, and so on from the least significant to the most significant, ending up with a sorted list. While the LSD radix sort requires the use of a stable sort, the MSD radix sort algorithm does not (unless stable sorting is desired). In-place MSD radix sort is not stable. It is common for the counting sortCounting sort
In computer science, counting sort is an algorithm for sorting a collection of objects according to keys that are small integers; that is, it is an integer sorting algorithm. It operates by counting the number of objects that have each distinct key value, and using arithmetic on those counts to...
algorithm to be used internally by the radix sort. Hybrid sorting approach, such as using insertion sort
Insertion sort
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort...
for small bins improves performance of radix sort significantly.
Distribution sort
Distribution sort refers to any sorting algorithm where data is distributed from its input to multiple intermediate structures which are then gathered and placed on the output. See Bucket sortBucket sort
Bucket sort, or bin sort, is a sorting algorithm that works by partitioning an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a distribution sort, and is a cousin of...
, Flashsort
Flashsort
Flashsort is a distribution sorting algorithm showing linear computational complexity O for uniformly distributed data sets and relatively little additional memory requirement...
.
Timsort
Timsort finds runs in the data, creates runs with insertion sort if necessary, and then uses merge sort to create the final sorted list. It has the same complexity (O(nlogn)) in the average and worst cases, but with pre-sorted data it goes down to O(n).Memory usage patterns and index sorting
When the size of the array to be sorted approaches or exceeds the available primary memory, so that (much slower) disk or swap space must be employed, the memory usage pattern of a sorting algorithm becomes important, and an algorithm that might have been fairly efficient when the array fit easily in RAM may become impractical. In this scenario, the total number of comparisons becomes (relatively) less important, and the number of times sections of memory must be copied or swapped to and from the disk can dominate the performance characteristics of an algorithm. Thus, the number of passes and the localization of comparisons can be more important than the raw number of comparisons, since comparisons of nearby elements to one another happen at system busComputer bus
In computer architecture, a bus is a subsystem that transfers data between components inside a computer, or between computers.Early computer buses were literally parallel electrical wires with multiple connections, but the term is now used for any physical arrangement that provides the same...
speed (or, with caching, even at CPU
Central processing unit
The central processing unit is the portion of a computer system that carries out the instructions of a computer program, to perform the basic arithmetical, logical, and input/output operations of the system. The CPU plays a role somewhat analogous to the brain in the computer. The term has been in...
speed), which, compared to disk speed, is virtually instantaneous.
For example, the popular recursive quicksort algorithm provides quite reasonable performance with adequate RAM, but due to the recursive way that it copies portions of the array it becomes much less practical when the array does not fit in RAM, because it may cause a number of slow copy or move operations to and from disk. In that scenario, another algorithm may be preferable even if it requires more total comparisons.
One way to work around this problem, which works well when complex records (such as in a relational database
Relational database
A relational database is a database that conforms to relational model theory. The software used in a relational database is called a relational database management system . Colloquial use of the term "relational database" may refer to the RDBMS software, or the relational database itself...
) are being sorted by a relatively small key field, is to create an index into the array and then sort the index, rather than the entire array. (A sorted version of the entire array can then be produced with one pass, reading from the index, but often even that is unnecessary, as having the sorted index is adequate.) Because the index is much smaller than the entire array, it may fit easily in memory where the entire array would not, effectively eliminating the disk-swapping problem. This procedure is sometimes called "tag sort".
Another technique for overcoming the memory-size problem is to combine two algorithms in a way that takes advantages of the strength of each to improve overall performance. For instance, the array might be subdivided into chunks of a size that will fit easily in RAM (say, a few thousand elements), the chunks sorted using an efficient algorithm (such as quicksort or heapsort
Heapsort
Heapsort is a comparison-based sorting algorithm to create a sorted array , and is part of the selection sort family. Although somewhat slower in practice on most machines than a well implemented quicksort, it has the advantage of a more favorable worst-case O runtime...
), and the results merged as per mergesort. This is less efficient than just doing mergesort in the first place, but it requires less physical RAM (to be practical) than a full quicksort on the whole array.
Techniques can also be combined. For sorting very large sets of data that vastly exceed system memory, even the index may need to be sorted using an algorithm or combination of algorithms designed to perform reasonably with virtual memory
Virtual memory
In computing, virtual memory is a memory management technique developed for multitasking kernels. This technique virtualizes a computer architecture's various forms of computer data storage , allowing a program to be designed as though there is only one kind of memory, "virtual" memory, which...
, i.e., to reduce the amount of swapping required.
Inefficient/humorous sorts
These are algorithms that are extremely slow compared to those discussed above — BogosortBogosort
In computer science, bogosort is a particularly ineffective sorting algorithm based on the generate and test paradigm. It is not useful for sorting, but may be used for educational purposes, to contrast it with other more realistic algorithms; it has also been used as an example in logic programming...
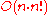 , Stooge sort
, Stooge sortStooge sort
Stooge sort is a recursive sorting algorithm with a time complexity of ).The running time of the algorithm is thus extremely slow comparedto efficient sorting algorithms, such as Merge sort, and is even slower than Bubble sort, a canonical example of a fairly inefficient and simple sort.The...
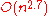 .
.See also
- External sortingExternal sortingExternal sorting is a term for a class of sorting algorithms that can handle massive amounts of data. External sorting is required when the data being sorted do not fit into the main memory of a computing device and instead they must reside in the slower external memory . External sorting...
- Sorting networkSorting networkA sorting network is an abstract mathematical model of a network of wires and comparator modules that is used to sort a sequence of numbers. Each comparator connects two wires and sorts the values by outputting the smaller value to one wire, and the larger to the other...
s (compare) - Cocktail sortCocktail sortCocktail sort, also known as bidirectional bubble sort, cocktail shaker sort, shaker sort , ripple sort, shuffle sort, shuttle sort or happy hour sort, is a variation of bubble sort that is both a stable sorting algorithm and a comparison sort...
- CollationCollationCollation is the assembly of written information into a standard order. One common type of collation is called alphabetization, though collation is not limited to ordering letters of the alphabet...
- Schwartzian transformSchwartzian transformIn computer science, the Schwartzian transform is a Perl programming idiom used to improve the efficiency of sorting a list of items. This idiom is appropriate for comparison-based sorting when the ordering is actually based on the ordering of a certain property of the elements, where computing...
- Shuffling algorithms
- Search algorithmSearch algorithmIn computer science, a search algorithm is an algorithm for finding an item with specified properties among a collection of items. The items may be stored individually as records in a database; or may be elements of a search space defined by a mathematical formula or procedure, such as the roots...
s
External links
- Sorting Algorithm Animations - Graphical illustration of how different algorithms handle different kinds of data sets.
- Sequential and parallel sorting algorithms - Explanations and analyses of many sorting algorithms.
- Dictionary of Algorithms, Data Structures, and Problems - Dictionary of algorithms, techniques, common functions, and problems.
- Slightly Skeptical View on Sorting Algorithms Discusses several classic algorithms and promotes alternatives to the quicksort algorithm.

