Selection sort is a sorting algorithm

Sorting algorithm

In computer science, a sorting algorithm is an algorithm that puts elements of a list in a certain order. The most-used orders are numerical order and lexicographical order...

, specifically an in-place

In-place algorithm

In computer science, an in-place algorithm is an algorithm which transforms input using a data structure with a small, constant amount of extra storage space. The input is usually overwritten by the output as the algorithm executes...

 comparison sort

Comparison sort

A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list...

. It has O

Big O notation

In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...

(n²) time complexity, making it inefficient on large lists, and generally performs worse than the similar insertion sort

Insertion sort

Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort...

. Selection sort is noted for its simplicity, and also has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.

Algorithm

The algorithm works as follows:

1. Find the minimum value in the list
2. Swap it with the value in the first position
3. Repeat the steps above for the remainder of the list (starting at the second position and advancing each time)

Effectively, the list is divided into two parts: the sublist of items already sorted, which is built up from left to right and is found at the beginning, and the sublist of items remaining to be sorted, occupying the remainder of the array.

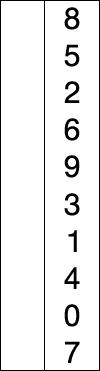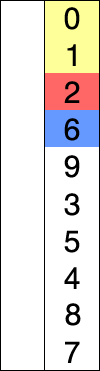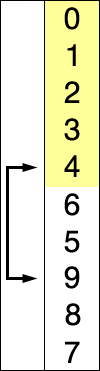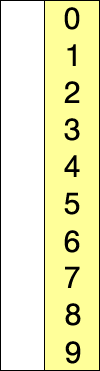
Here is an example of this sort algorithm sorting five elements:

64 25 12 22 11



11 25 12 22 64



11 12 25 22 64



11 12 22 25 64



11 12 22 25 64

(nothing appears changed on this last line because the last 2 numbers were already in order)

Selection sort can also be used on list structures that make add and remove efficient, such as a linked list

Linked list

In computer science, a linked list is a data structure consisting of a group of nodes which together represent a sequence. Under the simplest form, each node is composed of a datum and a reference to the next node in the sequence; more complex variants add additional links...

. In this case it is more common to remove the minimum element from the remainder of the list, and then insert it at the end of the values sorted so far. For example:

64 25 12 22 11



11 64 25 12 22



11 12 64 25 22



11 12 22 64 25



11 12 22 25 64

/* a[0] to a[n-1] is the array to sort */
int iPos;
int iMin;

/* advance the position through the entire array */
/* (could do iPos < n-1 because single element is also min element) */
for (iPos = 0; iPos < n; iPos++) {
/* find the min element in the unsorted a[iPos .. n-1] */

/* assume the min is the first element */
iMin = iPos;
/* test against all other elements */
for (i = iPos+1; i < n; i++) {
/* if this element is less, then it is the new minimum */
if (a[i] < a[iMin]) {
/* found new minimum; remember its index */
iMin = i;
}
}

/* iMin is the index of the minimum element. Swap it with the current position */
if ( iMin != iPos ) {
swap(a, iPos, iMin);
}
}

Mathematical definition

Let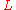 be a non-empty set and 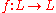such that 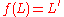where:

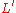1. is a permutation
   Permutation
   In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
   
    of ,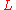
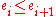2. for all 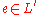and ,
3. ,
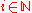   1. is the smallest element
      Maxima and minima
      In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
      
       of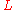 , and
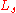   2. is the set of elements of 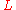without one instance of the smallest element of .
   
   

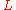   Analysis

   Selection sort is not difficult to analyze compared to other sorting algorithms since none of the loops depend on the data in the array. Selecting the lowest element requires scanning all n elements (this takes n − 1 comparisons) and then swapping it into the first position. Finding the next lowest element requires scanning the remaining n − 1 elements and so on, for (n − 1) + (n − 2) + ... + 2 + 1 = n(n − 1) / 2 ∈ Θ(n²) comparisons (see arithmetic progression
   Arithmetic progression
   In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
   
   ). Each of these scans requires one swap for n − 1 elements (the final element is already in place).
   

   Comparison to other sorting algorithms

   Among simple average-case Θ(n²) algorithms, selection sort almost always outperforms bubble sort
   Bubble sort
   Bubble sort, also known as sinking sort, is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which...
   
    and gnome sort
   Gnome sort
   Gnome sort, originally proposed by Hamid Sarbazi-Azad in 2000 and called , and then later on described by Dick Grune and named "Gnome sort", is a sorting algorithm which is similar to insertion sort, except that moving an element to its proper place is accomplished by a series of swaps, as in...
   
   , but is generally outperformed by insertion sort
   Insertion sort
   Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort...
   
   . Insertion sort is very similar in that after the kth iteration, the first k elements in the array are in sorted order. Insertion sort's advantage is that it only scans as many elements as it needs in order to place the k + 1st element, while selection sort must scan all remaining elements to find the k + 1st element.
   
   Simple calculation shows that insertion sort will therefore usually perform about half as many comparisons as selection sort, although it can perform just as many or far fewer depending on the order the array was in prior to sorting. It can be seen as an advantage for some real-time
   Real-time computing
   In computer science, real-time computing , or reactive computing, is the study of hardware and software systems that are subject to a "real-time constraint"— e.g. operational deadlines from event to system response. Real-time programs must guarantee response within strict time constraints...
   
    applications that selection sort will perform identically regardless of the order of the array, while insertion sort's running time can vary considerably. However, this is more often an advantage for insertion sort in that it runs much more efficiently if the array is already sorted or "close to sorted."
   
   While selection sort is preferable to insertion sort in terms of number of writes (Θ(n) swaps versus Ο(n²) swaps), it almost always far exceeds (and never beats) the number of writes that cycle sort
   Cycle sort
   Cycle sort is an in-place, unstable sorting algorithm, a comparison sort that is theoretically optimal in terms of the total number of writes to the original array, unlike any other in-place sorting algorithm...
   
    makes, as cycle sort is theoretically optimal in the number of writes. This can be important if writes are significantly more expensive than reads, such as with EEPROM
   EEPROM
   EEPROM stands for Electrically Erasable Programmable Read-Only Memory and is a type of non-volatile memory used in computers and other electronic devices to store small amounts of data that must be saved when power is removed, e.g., calibration...
   
    or Flash
   Flash memory
   Flash memory is a non-volatile computer storage chip that can be electrically erased and reprogrammed. It was developed from EEPROM and must be erased in fairly large blocks before these can be rewritten with new data...
   
    memory, where every write lessens the lifespan of the memory.
   
   Finally, selection sort is greatly outperformed on larger arrays by Θ(n log n) divide-and-conquer algorithms
   Divide and conquer algorithm
   In computer science, divide and conquer is an important algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same type, until these become simple enough to be solved directly...
   
    such as mergesort. However, insertion sort or selection sort are both typically faster for small arrays (i.e. fewer than 10–20 elements). A useful optimization in practice for the recursive algorithms is to switch to insertion sort or selection sort for "small enough" sublists.
   

   Variants

   Heapsort
   Heapsort
   Heapsort is a comparison-based sorting algorithm to create a sorted array , and is part of the selection sort family. Although somewhat slower in practice on most machines than a well implemented quicksort, it has the advantage of a more favorable worst-case O runtime...
   
    greatly improves the basic algorithm by using an implicit
   Implicit data structure
   In computer science, an implicit data structure is a data structure that uses very little memory besides the actual data elements i.e. very little information other than main data is stored in these structures. These are storage schemes which retain no pointers and represent the file of n k-key...
   
    heap
   Heap (data structure)
   In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: if B is a child node of A, then key ≥ key. This implies that an element with the greatest key is always in the root node, and so such a heap is sometimes called a max-heap...
   
    data structure
   Data structure
   In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
   
    to speed up finding and removing the lowest datum. If implemented correctly, the heap will allow finding the next lowest element in Θ(log n) time instead of Θ(n) for the inner loop in normal selection sort, reducing the total running time to Θ(n log n).
   
   A bidirectional variant of selection sort, called cocktail sort, is an algorithm which finds both the minimum and maximum values in the list in every pass. This reduces the number of scans of the list by a factor of 2, eliminating some loop overhead but not actually decreasing the number of comparisons or swaps. Note, however, that cocktail sort
   Cocktail sort
   Cocktail sort, also known as bidirectional bubble sort, cocktail shaker sort, shaker sort , ripple sort, shuffle sort, shuttle sort or happy hour sort, is a variation of bubble sort that is both a stable sorting algorithm and a comparison sort...
   
    more often refers to a bidirectional variant of bubble sort.
   
   Selection sort can be implemented as a stable sort. If, rather than swapping in step 2, the minimum value is inserted into the first position (that is, all intervening items moved down), the algorithm is stable. However, this modification either requires a data structure that supports efficient insertions or deletions, such as a linked list, or it leads to performing Θ(n²) writes.
   
   In the bingo sort variant, items are ordered by repeatedly looking through the remaining items to find the greatest value and moving all items with that value to their final location. Like counting sort
   Counting sort
   In computer science, counting sort is an algorithm for sorting a collection of objects according to keys that are small integers; that is, it is an integer sorting algorithm. It operates by counting the number of objects that have each distinct key value, and using arithmetic on those counts to...
   
   , this is an efficient variant if there are many duplicate values. Indeed, selection sort does one pass through the remaining items for each item moved. Bingo sort does one pass for each value (not item): after an initial pass to find the biggest value, the next passes can move every item with that value to its final location while finding the next value as in the following pseudocode
   Pseudocode
   In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
   
    (arrays are zero-based and the for-loop includes both the top and bottom limits, as in Pascal
   Pascal (programming language)
   Pascal is an influential imperative and procedural programming language, designed in 1968/9 and published in 1970 by Niklaus Wirth as a small and efficient language intended to encourage good programming practices using structured programming and data structuring.A derivative known as Object Pascal...
   
   ):
   
   
   bingo(array A)
   
   { This procedure sorts in ascending order. }
   begin
   max := length(A)-1;
   
   { The first iteration is written to look very similar to the subsequent ones, but
   without swaps. }
   nextValue := A[max];
   for i := max - 1 downto 0 do
   if A[i] > nextValue then
   nextValue := A[i];
   while (max > 0) and (A[max] = nextValue) do
   max := max - 1;
   
   while max > 0 do begin
   value := nextValue;
   nextValue := A[max];
   for i := max - 1 downto 0 do
   if A[i] = value then begin
   swap(A[i], A[max]);
   max := max - 1;
   end else if A[i] > nextValue then
   nextValue := A[i];
   while (max > 0) and (A[max] = nextValue) do
   max := max - 1;
   end;
   end;
   
   
   Thus if on average there are more than two items with each value, bingo sort can be expected to be faster, because it executes the inner loop fewer times than selection sort.
   
   

   External links

   • Animated Sorting Algorithms: Selection Sort – graphical demonstration and discussion of selection sort
   The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.