In computer science

Computer science

Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

, a self-balancing (or height-balanced) binary search tree is any node

Node (computer science)

A node is a record consisting of one or more fields that are links to other nodes, and a data field. The link and data fields are often implemented by pointers or references although it is also quite common for the data to be embedded directly in the node. Nodes are used to build linked, often...

 based binary search tree

Binary search tree

In computer science, a binary search tree , which may sometimes also be called an ordered or sorted binary tree, is a node-based binary tree data structurewhich has the following properties:...

 that automatically keeps its height (number of levels below the root) small in the face of arbitrary item insertions and deletions.

These structures provide efficient implementations for mutable ordered lists, and can be used for other abstract data structures such as associative arrays, priority queue

Priority queue

A priority queue is an abstract data type in computer programming.It is exactly like a regular queue or stack data structure, but additionally, each element is associated with a "priority"....

s and sets

Set (computer science)

In computer science, a set is an abstract data structure that can store certain values, without any particular order, and no repeated values. It is a computer implementation of the mathematical concept of a finite set...

.

Overview

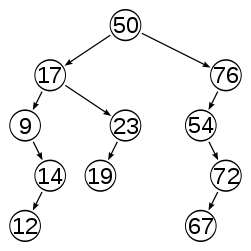
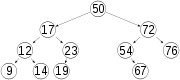
Most operations on a binary search tree (BST) take time directly proportional to the height of the tree, so it is desirable to keep the height small. A binary tree with height h can contain at most 2⁰+2¹+···+2^h = 2^h+1−1 nodes. It follows that for a tree with n nodes and height h: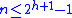



And that implies:

.

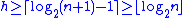In other words, the minimum height of a tree with n nodes is log

Logarithm

The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...

₂(n), rounded down; that is, :.

However, the simplest algorithms for BST item insertion may yield a tree with height n in rather common situations. For example, when the items are inserted in sorted key order, the tree degenerates into a linked list

Linked list

In computer science, a linked list is a data structure consisting of a group of nodes which together represent a sequence. Under the simplest form, each node is composed of a datum and a reference to the next node in the sequence; more complex variants add additional links...

 with n nodes. The difference in performance between the two situations may be enormous: for n = 1,000,000, for example, the minimum height is .

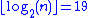If the data items are known ahead of time, the height can be kept small, in the average sense, by adding values in a random order, resulting in a random binary search tree. However, there are many situations (such as online algorithm

Online algorithm

In computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start. In contrast, an offline algorithm is given the whole problem data from...

s) where this randomization

Randomized algorithm

A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...

 is not viable.

Self-balancing binary trees solve this problem by performing transformations on the tree (such as tree rotation

Tree rotation

A tree rotation is an operation on a binary tree that changes the structure without interfering with the order of the elements. A tree rotation moves one node up in the tree and one node down...

s) at key times, in order to keep the height proportional to log₂(n). Although a certain overhead

Overhead

Overhead may be:* Overhead , the ongoing operating costs of running a business* Engineering overhead, ancillary design features required by a component of a device...

 is involved, it may be justified in the long run by ensuring fast execution of later operations.

Maintaining the height always at its minimum value is not always viable; it can be proven that any insertion algorithm which did so would have an excessive overhead. Therefore, most self-balanced BST algorithms keep the height within a constant factor of this lower bound.

In the asymptotic ("Big-O

Big O notation

In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...

") sense, a self-balancing BST structure containing n items allows the lookup, insertion, and removal of an item in O(log n) worst-case time, and ordered enumeration of all items in O(n) time. For some implementations these are per-operation time bounds, while for others they are amortized

Amortized analysis

In computer science, amortized analysis is a method of analyzing algorithms that considers the entire sequence of operations of the program. It allows for the establishment of a worst-case bound for the performance of an algorithm irrespective of the inputs by looking at all of the operations...

 bounds over a sequence of operations. These times are asymptotically optimal among all data structures that manipulate the key only through comparisons.

Implementations

Popular data structures implementing this type of tree include:

• AA tree
  AA tree
  An AA tree in computer science is a form of balanced tree used for storing and retrieving ordered data efficiently. AA trees are named for Arne Andersson, their inventor....
  
  
• AVL tree
  AVL tree
  In computer science, an AVL tree is a self-balancing binary search tree, and it was the first such data structure to be invented. In an AVL tree, the heights of the two child subtrees of any node differ by at most one. Lookup, insertion, and deletion all take O time in both the average and worst...
  
  
• Red-black tree
  Red-black tree
  A red–black tree is a type of self-balancing binary search tree, a data structure used in computer science, typically to implement associative arrays. The original structure was invented in 1972 by Rudolf Bayer and named "symmetric binary B-tree," but acquired its modern name in a paper in 1978 by...
  
  
• Scapegoat tree
  Scapegoat tree
  In computer science, a scapegoat tree is a self-balancing binary search tree, discovered by Arne Anderson and again by Igal Galperin and Ronald L. Rivest...
  
  
• Splay tree
  Splay tree
  A splay tree is a self-adjusting binary search tree with the additional property that recently accessed elements are quick to access again. It performs basic operations such as insertion, look-up and removal in O amortized time. For many sequences of nonrandom operations, splay trees perform...
  
  
• Treap
  Treap
  In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys...
  
  

Applications

Self-balancing binary search trees can be used in a natural way to construct and maintain ordered lists, such as priority queue

Priority queue

A priority queue is an abstract data type in computer programming.It is exactly like a regular queue or stack data structure, but additionally, each element is associated with a "priority"....

s. They can also be used for associative array

Associative array

In computer science, an associative array is an abstract data type composed of a collection of pairs, such that each possible key appears at most once in the collection....

s; key-value pairs are simply inserted with an ordering based on the key alone. In this capacity, self-balancing BSTs have a number of advantages and disadvantages over their main competitor, hash table

Hash table

In computer science, a hash table or hash map is a data structure that uses a hash function to map identifying values, known as keys , to their associated values . Thus, a hash table implements an associative array...

s. One advantage of self-balancing BSTs is that they allow fast (indeed, asymptotically optimal) enumeration of the items in key order, which hash tables do not provide. One disadvantage is that their lookup algorithms get more complicated when there may be multiple items with the same key.

Self-balancing BSTs can be used to implement any algorithm that requires mutable ordered lists, to achieve optimal worst-case asymptotic performance. For example, if binary tree sort is implemented with a self-balanced BST, we have a very simple-to-describe yet asymptotically optimal

Asymptotically optimal

In computer science, an algorithm is said to be asymptotically optimal if, roughly speaking, for large inputs it performs at worst a constant factor worse than the best possible algorithm...

 O(n log n) sorting algorithm. Similarly, many algorithms in computational geometry

Computational geometry

Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...

 exploit variations on self-balancing BSTs to solve problems such as the line segment intersection

Line segment intersection

In computational geometry, the line segment intersection problem supplies a list of line segments in the plane and asks us to determine whether any two of them intersect, or cross....

 problem and the point location

Point location

The point location problem is a fundamental topic of computational geometry. It finds applications in areas that deal with processing geometrical data: computer graphics, geographic information systems , motion planning, and computer aided design ....

 problem efficiently. (For average-case performance, however, self-balanced BSTs may be less efficient than other solutions. Binary tree sort, in particular, is likely to be slower than mergesort or quicksort, because of the tree-balancing overhead as well as cache access patterns.)

Self-balancing BSTs are flexible data structures, in that it's easy to extend them to efficiently record additional information or perform new operations. For example, one can record the number of nodes in each subtree having a certain property, allowing one to count the number of nodes in a certain key range with that property in O(log n) time. These extensions can be used, for example, to optimize database queries or other list-processing algorithms.

External links

• Dictionary of Algorithms and Data Structures: Height-balanced binary search tree
• GNU libavl, a LGPL-licensed library of binary tree implementations in C, with documentation