Set (computer science)
Encyclopedia
In computer science
, a set is an abstract data structure that can store certain values, without any particular order
, and no repeated values. It is a computer implementation of the mathematical
concept of a finite set. Unlike most other collection types, rather than retrieving a specific element from a set, one typically tests a value for membership in a set.
Some set data structures are designed for static or frozen sets that do not change after they are constructed. Static sets allow only query operations on their elements — such as checking whether a given value is in the set, or enumerating the values in some arbitrary order. Other variants, called dynamic or mutable sets, allow also the insertion and/or deletion of elements from the set.
A set can be implemented in many ways. For example, one can use a list, ignoring the order of the elements and taking care to avoid repeated values. Sets are often implemented using various flavors of trees
, trie
s, or hash tables.
A set can be seen, and implemented, as a (partial) associative array
, in which the value of each key-value pair has the unit type
.
In type theory
, sets are generally identified with their indicator function: accordingly, a set of values of type
may be denoted by 
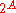or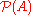 
. (Subtypes and subsets may be modeled by refinement types, and quotient sets may be replaced by setoid
s.) The characteristic function F of a set S is defined as: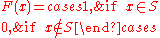
In theory, many other abstract data structures can be viewed as set structures with additional operations and/or additional axiom
s imposed on the standard operations. For example, an abstract heap can be viewed as a set structure with a
:
Some set structures may allow only some of these operations. The cost of each operation will depend on the implementation, and possibly also on the particular values stored in the set, and the order in which they are inserted.
Other operations can be defined for sets with elements of a special type:
s, which provide different time and space trade-offs for various operations. Some implementations are designed to improve the efficiency of very specialized operations, such as
Sets are commonly implemented in the same way as associative arrays, namely, a self-balancing binary search tree
for sorted sets (which has O(log n) for most operations), or a hash table
for unsorted sets (which has O(1) average-case, but O(n) worst-case, for most operations). A sorted linear hash table may be used to provide deterministically ordered sets.
Other popular methods include arrays. In particular a subset of the integers 1..n can be implemented efficiently as an n-bit bit array, which also support very efficient union and intersection operations. A Bloom map implements a set probabilistically, using a very compact representation but risking a small chance of false positives on queries.
The Boolean set operations can be implemented in terms of more elementary operations (
will do the job in time proportional to m+n. Moreover, there are specialized set data structures (such as the union-find data structure) that are optimized for one or more of these operations, at the expense of others.
.
As noted in the previous section, in languages which do not directly support sets but do support associative array
s, sets can be emulated using associative arrays, by using the elements as keys, and using a dummy value as the values, which are ignored.
, the Standard Template Library
(STL) provides the
's STL also provides the
In sets, the elements themselves are the keys, in contrast to sequenced containers, where elements are accessed using their (relative or absolute) position. Set elements must have a strict weak ordering.
Some of the member functions in C++ and their description is given in the table below:
or bag, which is the same as a set data structure, but allows repeated ("equal") values. It is possible for objects in computer science to be considered "equal" under some equivalence relation
but still distinct under another relation. Some types of multiset implementations will store distinct equal objects as separate items in the data structure; while others will collapse it down to one version (the first one encountered) and keep a positive integer count of the multiplicity of the element.
Where a multiset data structure is not available, a workaround is to use a regular set, but override the equality predicate of its items to always return "not equal" on distinct objects (however, such will still not be able to store multiple occurrences of the same object) or use an associative array
mapping the values to their integer multiplicities (this will not be able to distinguish between equal elements at all).
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a set is an abstract data structure that can store certain values, without any particular order
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
, and no repeated values. It is a computer implementation of the mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
concept of a finite set. Unlike most other collection types, rather than retrieving a specific element from a set, one typically tests a value for membership in a set.
Some set data structures are designed for static or frozen sets that do not change after they are constructed. Static sets allow only query operations on their elements — such as checking whether a given value is in the set, or enumerating the values in some arbitrary order. Other variants, called dynamic or mutable sets, allow also the insertion and/or deletion of elements from the set.
A set can be implemented in many ways. For example, one can use a list, ignoring the order of the elements and taking care to avoid repeated values. Sets are often implemented using various flavors of trees
Tree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
, trie
Trie
In computer science, a trie, or prefix tree, is an ordered tree data structure that is used to store an associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the...
s, or hash tables.
A set can be seen, and implemented, as a (partial) associative array
Associative array
In computer science, an associative array is an abstract data type composed of a collection of pairs, such that each possible key appears at most once in the collection....
, in which the value of each key-value pair has the unit type
Unit type
In the area of mathematical logic, and computer science known as type theory, a unit type is a type that allows only one value . The carrier associated with a unit type can be any singleton set. There is an isomorphism between any two such sets, so it is customary to talk about the unit type and...
.
In type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
, sets are generally identified with their indicator function: accordingly, a set of values of type
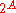may be denoted by or 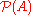. (Subtypes and subsets may be modeled by refinement types, and quotient sets may be replaced by setoidSetoid
In mathematics, a setoid is a set equipped with an equivalence relation.Setoids are studied especially in proof theory and in type-theoretic foundations of mathematics. Often in mathematics, when one defines an equivalence relation on a set, one immediately forms the quotient set...
s.) The characteristic function F of a set S is defined as:
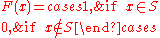
In theory, many other abstract data structures can be viewed as set structures with additional operations and/or additional axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s imposed on the standard operations. For example, an abstract heap can be viewed as a set structure with a
min(S) operation that returns the element of smallest value.Core set-theoretical operations
One may define the operations of the algebra of setsAlgebra of sets
The algebra of sets develops and describes the basic properties and laws of sets, the set-theoretic operations of union, intersection, and complementation and the relations of set equality and set inclusion...
:
-
union(S,T): returns the unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of sets S and T. -
intersection(S,T): returns the intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of sets S and T. -
difference(S,T): returns the difference of sets S and T. -
subset(S,T): a predicate that tests whether the set S is a subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of set T.
Static sets
Typical operations that may be provided by a static set structure S are:-
is_element_of(x,S): checks whether the value x is in the set S. -
is_empty(S): checks whether the set S is empty. -
size(S)orcardinality(S): returns the number of elements in S. -
iterate: returns a function that returns one more value of S at each call, in some arbitrary order.IteratorIn computer programming, an iterator is an object that enables a programmer to traverse a container. Various types of iterators are often provided via a container's interface...
(S) -
enumerate(S): returns a list containing the elements of S in some arbitrary order. -
build(x1,x2,…,xn,): creates a set structure with values x1,x2,…,xn. -
create_from(collection): creates a new set structure containing all the elements of the given collectionCollection (computing)In computer science, a collection is a grouping of some variable number of data items that have some shared significance to the problem being solved and need to be operated upon together in some controlled fashion. Generally, the data items will be of the same type or, in languages supporting...
or all the elements returned by the given iteratorIteratorIn computer programming, an iterator is an object that enables a programmer to traverse a container. Various types of iterators are often provided via a container's interface...
.
Dynamic sets
Dynamic set structures typically add:-
create: creates a new, initially empty set structure.-
create_with_capacity(n): creates a new set structure, initially empty but capable of holding up to n elements.
-
-
add(S,x): adds the element x to S, if it is not present already. -
remove(S, x): removes the element x from S, if it is present. -
capacity(S): returns the maximum number of values that S can hold.
Some set structures may allow only some of these operations. The cost of each operation will depend on the implementation, and possibly also on the particular values stored in the set, and the order in which they are inserted.
Additional operations
There are many other operations that can (in principle) be defined in terms of the above, such as:-
pop(S): returns an arbitrary element of S, deleting it from S. -
map: returns the set of distinct values resulting from applying function F to each element of S.Map (higher-order function)In many programming languages, map is the name of a higher-order function that applies a given function to each element of a list, returning a list of results. They are examples of both catamorphisms and anamorphisms...
(F,S) -
filter: returns the subset containing all elements of S that satisfy a given predicate P.Filter (higher-order function)In functional programming, filter is a higher-order function that processes a data structure in some order to produce a new data structure containing exactly those elements of the original data structure for which a given predicate returns the boolean value true.-Example:In Haskell, the code...
(P,S) -
fold: returns the value A|S| after applyingFold (higher-order function)In functional programming, fold – also known variously as reduce, accumulate, compress, or inject – are a family of higher-order functions that analyze a recursive data structure and recombine through use of a given combining operation the results of recursively processing its...
(A0,F,S)Ai+1 := F(Ai, e)for each element e of S. -
clear(S): delete all elements of S. -
equal(S1, S2): checks whether the two given sets are equal (i.e. contain all and only the same elements). -
hash(S): returns a hash value for the static set S such that ifequal(S1, S2)thenhash(S1) = hash(S2)
Other operations can be defined for sets with elements of a special type:
-
sum(S): returns the sum of all elements of S for some definition of "sum". For example, over integers or reals, it may be defined asfold(0, add, S). -
nearest(S,x): returns the element of S that is closest in value to x (by some metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
).
Implementations
Sets can be implemented using various data structureData structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
s, which provide different time and space trade-offs for various operations. Some implementations are designed to improve the efficiency of very specialized operations, such as
nearest or union. Implementations described as "general use" typically strive to optimize the element_of, add, and delete operations.Sets are commonly implemented in the same way as associative arrays, namely, a self-balancing binary search tree
Self-balancing binary search tree
In computer science, a self-balancing binary search tree is any node based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions....
for sorted sets (which has O(log n) for most operations), or a hash table
Hash table
In computer science, a hash table or hash map is a data structure that uses a hash function to map identifying values, known as keys , to their associated values . Thus, a hash table implements an associative array...
for unsorted sets (which has O(1) average-case, but O(n) worst-case, for most operations). A sorted linear hash table may be used to provide deterministically ordered sets.
Other popular methods include arrays. In particular a subset of the integers 1..n can be implemented efficiently as an n-bit bit array, which also support very efficient union and intersection operations. A Bloom map implements a set probabilistically, using a very compact representation but risking a small chance of false positives on queries.
The Boolean set operations can be implemented in terms of more elementary operations (
pop, clear, and add), but specialized algorithms may yield lower asymptotic time bounds. If sets are implemented as sorted lists, for example, the naive algorithm for union(S,T) will take code proportional to the length m of S times the length n of T; whereas a variant of the list merging algorithmMerge algorithm
Merge algorithms are a family of algorithms that run sequentially over multiple sorted lists, typically producing more sorted lists as output. This is well-suited for machines with tape drives...
will do the job in time proportional to m+n. Moreover, there are specialized set data structures (such as the union-find data structure) that are optimized for one or more of these operations, at the expense of others.
Language support
One of the earliest languages to support sets was Pascal; many languages now include it, whether in the core language or in a standard libraryStandard library
A standard library for a programming language is the library that is conventionally made available in every implementation of that language. In some cases, the library is described directly in the programming language specification; in other cases, the contents of the standard library are...
.
- JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
offers the interfaceInterface (computer science)In the field of computer science, an interface is a tool and concept that refers to a point of interaction between components, and is applicable at the level of both hardware and software...
to support sets (with the class implementing it using a hash table), and the sub-interface to support sorted sets (with the class implementing it using a binary search tree). - Apple's Foundation frameworkFoundation KitThe Foundation Kit, or just Foundation for short, is an Objective-C framework in the OpenStep specification. It provides basic classes such as wrapper classes and data structure classes. This framework uses the prefix NS .-NSObject:...
(part of CocoaCocoa (API)Cocoa is Apple's native object-oriented application programming interface for the Mac OS X operating system and—along with the Cocoa Touch extension for gesture recognition and animation—for applications for the iOS operating system, used on Apple devices such as the iPhone, the iPod Touch, and...
) provides the Objective-CObjective-CObjective-C is a reflective, object-oriented programming language that adds Smalltalk-style messaging to the C programming language.Today, it is used primarily on Apple's Mac OS X and iOS: two environments derived from the OpenStep standard, though not compliant with it...
classesNSSet,NSMutableSet,NSCountedSet,NSOrderedSet, andNSMutableOrderedSet. The CoreFoundation APIs provide the CFSet and CFMutableSet types for use in CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
. - PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
has built-insetandfrozensettypes since 2.4, and since Python 3.0 and 2.7, supports non-empty set literals using a curly-bracket syntax, e.g.:{ x, y, z }. - The .NET Framework.NET FrameworkThe .NET Framework is a software framework that runs primarily on Microsoft Windows. It includes a large library and supports several programming languages which allows language interoperability...
provides the genericHashSetandSortedSetclasses that implement the genericISetinterface. - RubyRuby (programming language)Ruby is a dynamic, reflective, general-purpose object-oriented programming language that combines syntax inspired by Perl with Smalltalk-like features. Ruby originated in Japan during the mid-1990s and was first developed and designed by Yukihiro "Matz" Matsumoto...
's standard library includes asetmodule which containsSetandSortedSetclasses that implement sets using hash tables, the latter allowing iteration in sorted order. - OCaml's standard library contains a
Setmodule, which implements a functional set data structure using binary search trees. - The GHCGlasgow Haskell CompilerThe Glorious Glasgow Haskell Compilation System, more commonly known as the Glasgow Haskell Compiler or GHC, is an open source native code compiler for the functional programming language Haskell. The lead developers are Simon Peyton Jones and Simon Marlow...
implementation of HaskellHaskell (programming language)Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
provides aData.Setmodule, which implements a functional set data structure using binary search trees. - The TclTclTcl is a scripting language created by John Ousterhout. Originally "born out of frustration", according to the author, with programmers devising their own languages intended to be embedded into applications, Tcl gained acceptance on its own...
TcllibTcllibTcllib is a collection of packages available for the Tcl programming language. Tcllib is distributed in both source code as well as pre-compiled binary formats...
package provides a set module which implements a set data structure based upon TCL lists.
As noted in the previous section, in languages which do not directly support sets but do support associative array
Associative array
In computer science, an associative array is an abstract data type composed of a collection of pairs, such that each possible key appears at most once in the collection....
s, sets can be emulated using associative arrays, by using the elements as keys, and using a dummy value as the values, which are ignored.
In C++
In C++C++
C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
, the Standard Template Library
Standard Template Library
The Standard Template Library is a C++ software library which later evolved into the C++ Standard Library. It provides four components called algorithms, containers, functors, and iterators. More specifically, the C++ Standard Library is based on the STL published by SGI. Both include some...
(STL) provides the
set template class, which implements a sorted set using a binary search tree; SGISilicon Graphics International
Silicon Graphics International Corp. , is an American manufacturer of computer hardware and software, including high-performance computing solutions, x86-based servers for datacenter deployment, and visualization products...
's STL also provides the
hash_set template class, which implements a set using a hash table.In sets, the elements themselves are the keys, in contrast to sequenced containers, where elements are accessed using their (relative or absolute) position. Set elements must have a strict weak ordering.
Some of the member functions in C++ and their description is given in the table below:
| Signature(s) | Description |
|---|---|
iterator begin; |
Returns an iterator to the first element of the set. |
iterator end; |
Returns an iterator just before the end of the set. |
bool empty const; |
Checks if the set container is empty (i.e. has a size of 0) |
iterator find(const key_type &x) const; |
Searches the container for an element x and if found, returns an iterator to it, or else returns an iterator to set::end |
| |
Inserts an element into the set. The first version returns pair, with its member pair::first set to an iterator pointing to either the newly inserted element or to the element that already had its same value in the set. The pair::second element in the pair is set to true if a new element was inserted or false if an element with the same value existed. And the second version returns an iterator either pointing to newly inserted element or to element having same value in set. |
void clear; |
Removes all elements in the set, making its size 0. |
Template parameters
Herevalue_type and iterator are member types defined in set containers. Firstly, value to be used to initialize inserted element. Then position of first element compared for the operation.It actually does not give the position where element is to be inserted but just an indication of possible insertion position in the container so as to make efficient insertion operation. Template type can be any type of input iterator. Iterators specify a range of elements and copies of these in range [first, last) are inserted in set.Multiset
A variation of the set is the multisetMultiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
or bag, which is the same as a set data structure, but allows repeated ("equal") values. It is possible for objects in computer science to be considered "equal" under some equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
but still distinct under another relation. Some types of multiset implementations will store distinct equal objects as separate items in the data structure; while others will collapse it down to one version (the first one encountered) and keep a positive integer count of the multiplicity of the element.
- C++'s Standard Template Library provides the
multisetclass for the sorted multiset, and SGI's STL provides thehash_multisetclass, which implements a multiset using a hash table. - For JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
, third-party libraries provide multiset functionality: - Apple provides the
NSCountedSetclass as part of CocoaCocoa (API)Cocoa is Apple's native object-oriented application programming interface for the Mac OS X operating system and—along with the Cocoa Touch extension for gesture recognition and animation—for applications for the iOS operating system, used on Apple devices such as the iPhone, the iPod Touch, and...
, and theCFBagandCFMutableBagtypes as part of CoreFoundation. - Python'sPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
standard library includescollections.Counter, which is similar to a multiset.
Where a multiset data structure is not available, a workaround is to use a regular set, but override the equality predicate of its items to always return "not equal" on distinct objects (however, such will still not be able to store multiple occurrences of the same object) or use an associative array
Associative array
In computer science, an associative array is an abstract data type composed of a collection of pairs, such that each possible key appears at most once in the collection....
mapping the values to their integer multiplicities (this will not be able to distinguish between equal elements at all).