Green-Kubo relations
Encyclopedia
The Green–Kubo relations (Melville S. Green
1954, Ryogo Kubo
1957) give the exact mathematical expression for transport coefficients in terms of integrals of time correlation functions.
The standard example of a mechanical transport process would be Ohm's law
which states that at least for sufficiently small applied voltages, the current I is linearly proportional to the applied voltage V,
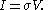
As the applied voltage increases we expect to see deviations from linear behaviour. The coefficient of proportionality is the electrical conductivity which is the reciprocal of the electrical resistance.
The standard example of a thermal transport process would be Newton's Law of viscosity
which states that the shear stress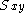
is linearly proportional to the strain rate. The strain rate 
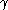is the rate of change streaming velocity in the x-direction, with respect to the y-coordinate, 
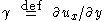. Newton's Law of viscosity states
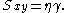
As the strain rate increases we expect to see deviations from linear behaviour
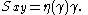
Another well known thermal transport process is Fourier's Law of Heat conduction
which states that the heat flux
between two bodies maintained at different temperatures is proportional to the temperature gradient (the temperature difference divided by the spatial separation).
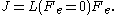
L(0) is called a linear transport coefficient.
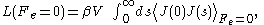
where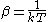
(with k the Boltzmann constant), and V is the system volume. The integral is over the equilibrium flux autocovariance
function. At zero time the autocovariance is positive since it is the mean square value of the flux at equilibrium. Note that at equilibrium the mean value of the flux is zero by definition. At long times the flux at time t, J(t), is uncorrelated with its value a long time earlier J(0) and the autocorrelation function decays to zero. This remarkable relation is frequently used in molecular dynamics computer simulation to compute linear transport coefficients; see Evans and Morriss, "Statistical Mechanics of Nonequilibrium Liquids", Academic Press 1990.
and Morriss derived two exact fluctuation expressions for nonlinear transport coefficients—see Evans and Morriss in Mol. Phys, 54, 629(1985). Evans later argued that these are consequences of the extremization of free energy
in Response theory as a free energy minimum.
Evans and Morriss proved that in a thermostatted system that is at equilibrium at t = 0, the nonlinear transport coefficient can be calculated from the so-called transient time correlation function expression:
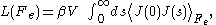
where the equilibrium (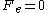
) flux autocorrelation function is replaced by a thermostatted field dependent transient autocorrelation function. At time zero 
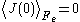but at later times since the field is applied 
.
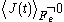Another exact fluctuation expression derived by Evans and Morriss is the so-called Kawasaki expression for the nonlinear response:
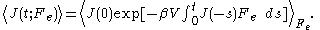
The ensemble average of the right hand side of the Kawasaki expression is to be evaluated under the application of both the thermostat and the external field. At first sight the transient time correlation function (TTCF) and Kawasaki expression might appear to be of limited use—because of their innate complexity. However, the TTCF is quite useful in computer simulations for calculating transport coefficients. Both expressions can be used to derive new and useful fluctuation expressions quantities like specific heats, in nonequilibrium steady states. Thus they can be used as a kind of partition function
for nonequilibrium steady states.
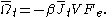
We note in passing that the long time average of the dissipation function is a product of the thermodynamic force and the average conjugate thermodynamic flux. It is therefore equal to the spontaneous entropy production in the system. The spontaneous entropy production plays a key role in linear irreversible thermodynamics - see de Groot and Mazur "Non-equilibrium thermodynamics" Dover.
The fluctuation theorem
(FT) is valid for arbitrary averaging times, t. Let's apply the FT in the long time limit while simultaneously reducing the field so that the product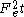
is held constant,
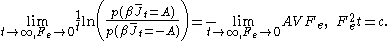
Because of the particular way we take the double limit, the negative of the mean value of the flux remains a fixed number of standard deviations away from the mean as the averaging time increases (narrowing the distribution) and the field decreases. This means that as the averaging time gets longer the distribution near the mean flux and its negative, is accurately described by the central limit theorem
. This means that the distribution is Gaussian near the mean and its negative so that
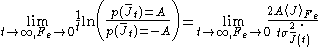
Combining these two relations yields (after some tedious algebra!) the exact Green–Kubo relation for the linear zero field transport coefficient, namely,
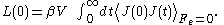
Details of the proof of Green–Kubo relations from the FT are here .
in nonequilibrium statistical mechanics.
The FT (together with the Axiom of Causality
) gives a generalisation of the Second Law of Thermodynamics
. It is then easy to prove the second law inequality and the Kawasaki identity. When combined with the central limit theorem
, the FT also implies the famous Green–Kubo relations for linear transport coefficients, close to equilibrium. The FT is however, more general than the Green–Kubo Relations because unlike them, the FT applies to fluctuations far from equilibrium. In spite of this fact, no one has yet been able to derive the equations for nonlinear response theory from the FT.
The FT does not imply or require that the distribution of time-averaged dissipation is Gaussian. There are many examples known when the distribution is non-Gaussian and yet the FT (of course) still correctly describes the probability ratios.
Melville S. Green
Melville S. Green was a statistical physicist.He is known for the Green-Kubo relations.He also worked on the Yvon–Born–Green hierarchy,which however is not named for him, but for Herbert S. Green....
1954, Ryogo Kubo
Ryogo Kubo
was a Japanese mathematical physicist, best known for his works in statistical physics and non-equilibrium statistical mechanics.In the early 1950s, Kubo transformed research into the linear response properties of near-equilibrium condensed-matter systems, in particular the understanding of...
1957) give the exact mathematical expression for transport coefficients in terms of integrals of time correlation functions.
Thermal and mechanical transport processes
Thermodynamic systems may be prevented from relaxing to equilibrium because of the application of a mechanical field (e.g. electric or magnetic field), or because the boundaries of the system are in relative motion (shear) or maintained at different temperatures, etc. This generates two classes of nonequilibrium system: mechanical nonequilibrium systems and thermal nonequilibrium systems.The standard example of a mechanical transport process would be Ohm's law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
which states that at least for sufficiently small applied voltages, the current I is linearly proportional to the applied voltage V,
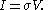
As the applied voltage increases we expect to see deviations from linear behaviour. The coefficient of proportionality is the electrical conductivity which is the reciprocal of the electrical resistance.
The standard example of a thermal transport process would be Newton's Law of viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
which states that the shear stress
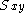is linearly proportional to the strain rate. The strain rate 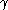is the rate of change streaming velocity in the x-direction, with respect to the y-coordinate, 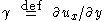. Newton's Law of viscosity states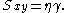As the strain rate increases we expect to see deviations from linear behaviour
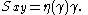
Another well known thermal transport process is Fourier's Law of Heat conduction
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
which states that the heat flux
Heat flux
Heat flux or thermal flux is the rate of heat energy transfer through a given surface. The SI derived unit of heat rate is joule per second, or watt. Heat flux is the heat rate per unit area. In SI units, heat flux is measured in W/m2]. Heat rate is a scalar quantity, while heat flux is a vectorial...
between two bodies maintained at different temperatures is proportional to the temperature gradient (the temperature difference divided by the spatial separation).
Linear constitutive relations
So regardless of whether transport processes are stimulated thermally or mechanically, in the small field limit it is expected that a flux will be linearly proportional to an applied field. In such a case the flux and the force are said to be conjugate to each other. The relation between a thermodynamic force F and its conjugate thermodynamic flux J is called a linear constitutive relation,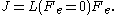L(0) is called a linear transport coefficient.
Green–Kubo relations
In the 1950s Green and Kubo proved an exact expression for linear transport coefficients which is valid for systems of arbitrary temperature, T, and density. They proved that linear transport coefficients are exactly related to the time dependence of equilibrium fluctuations in the conjugate flux,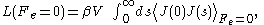where
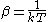(with k the Boltzmann constant), and V is the system volume. The integral is over the equilibrium flux autocovarianceAutocovariance
In statistics, given a real stochastic process X, the autocovariance is the covariance of the variable with itself, i.e. the variance of the variable against a time-shifted version of itself...
function. At zero time the autocovariance is positive since it is the mean square value of the flux at equilibrium. Note that at equilibrium the mean value of the flux is zero by definition. At long times the flux at time t, J(t), is uncorrelated with its value a long time earlier J(0) and the autocorrelation function decays to zero. This remarkable relation is frequently used in molecular dynamics computer simulation to compute linear transport coefficients; see Evans and Morriss, "Statistical Mechanics of Nonequilibrium Liquids", Academic Press 1990.
Nonlinear response and transient time correlation functions
In 1985 Denis EvansDenis Evans
Denis James Evans, , is a Professor in the Research School of Chemistry at the Australian National University...
and Morriss derived two exact fluctuation expressions for nonlinear transport coefficients—see Evans and Morriss in Mol. Phys, 54, 629(1985). Evans later argued that these are consequences of the extremization of free energy
Thermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
in Response theory as a free energy minimum.
Evans and Morriss proved that in a thermostatted system that is at equilibrium at t = 0, the nonlinear transport coefficient can be calculated from the so-called transient time correlation function expression:
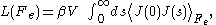
where the equilibrium (
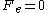) flux autocorrelation function is replaced by a thermostatted field dependent transient autocorrelation function. At time zero 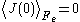but at later times since the field is applied 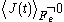.Another exact fluctuation expression derived by Evans and Morriss is the so-called Kawasaki expression for the nonlinear response:
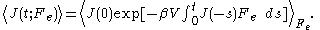
The ensemble average of the right hand side of the Kawasaki expression is to be evaluated under the application of both the thermostat and the external field. At first sight the transient time correlation function (TTCF) and Kawasaki expression might appear to be of limited use—because of their innate complexity. However, the TTCF is quite useful in computer simulations for calculating transport coefficients. Both expressions can be used to derive new and useful fluctuation expressions quantities like specific heats, in nonequilibrium steady states. Thus they can be used as a kind of partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
for nonequilibrium steady states.
Derivation from the fluctuation theorem and the central limit theorem
For a thermostatted steady state, time integrals of the dissipation function are related to the dissipative flux, J, by the equation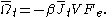We note in passing that the long time average of the dissipation function is a product of the thermodynamic force and the average conjugate thermodynamic flux. It is therefore equal to the spontaneous entropy production in the system. The spontaneous entropy production plays a key role in linear irreversible thermodynamics - see de Groot and Mazur "Non-equilibrium thermodynamics" Dover.
The fluctuation theorem
Fluctuation theorem
The fluctuation theorem , which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium will increase or decrease over a given amount of time...
(FT) is valid for arbitrary averaging times, t. Let's apply the FT in the long time limit while simultaneously reducing the field so that the product
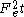is held constant,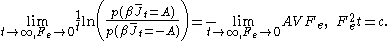Because of the particular way we take the double limit, the negative of the mean value of the flux remains a fixed number of standard deviations away from the mean as the averaging time increases (narrowing the distribution) and the field decreases. This means that as the averaging time gets longer the distribution near the mean flux and its negative, is accurately described by the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
. This means that the distribution is Gaussian near the mean and its negative so that
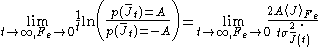
Combining these two relations yields (after some tedious algebra!) the exact Green–Kubo relation for the linear zero field transport coefficient, namely,
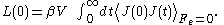
Details of the proof of Green–Kubo relations from the FT are here .
Summary
This shows the fundamental importance of the fluctuation theoremFluctuation theorem
The fluctuation theorem , which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium will increase or decrease over a given amount of time...
in nonequilibrium statistical mechanics.
The FT (together with the Axiom of Causality
Axiom of Causality
The Axiom of Causality is the proposition that everything in the universe has a cause and is thus an effect of that cause. This means that if a given event occurs, then this is the result of a previous, related event. If an object is in a certain state, then it is in that state as a result of...
) gives a generalisation of the Second Law of Thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
. It is then easy to prove the second law inequality and the Kawasaki identity. When combined with the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, the FT also implies the famous Green–Kubo relations for linear transport coefficients, close to equilibrium. The FT is however, more general than the Green–Kubo Relations because unlike them, the FT applies to fluctuations far from equilibrium. In spite of this fact, no one has yet been able to derive the equations for nonlinear response theory from the FT.
The FT does not imply or require that the distribution of time-averaged dissipation is Gaussian. There are many examples known when the distribution is non-Gaussian and yet the FT (of course) still correctly describes the probability ratios.
See also
- Density matrixDensity matrixIn quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
- Fluctuation theoremFluctuation theoremThe fluctuation theorem , which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium will increase or decrease over a given amount of time...
- Green's function (many-body theory)Green's function (many-body theory)In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators....
- Lindblad equationLindblad equationIn quantum mechanics, the Kossakowski–Lindblad equation or master equation in the Lindblad form is the most general type of markovian and time-homogeneous master equation describing non-unitary evolution of the density matrix \rho that is trace preserving and completely positive for any initial...
- Linear response functionLinear response functionA linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response...