
Gross–Koblitz formula
Encyclopedia
In mathematics the Gross–Koblitz formula, introduced by expresses a Gauss sum
using a product of values of the p-adic gamma function
. It is an analog of the Chowla–Selberg formula for the usual gamma function. It implies the Hasse–Davenport relation
and generalizes the Stickelberger theorem.
gave another proof of the Gross–Koblitz formula using Dwork's work, and
gave an elementary proof.
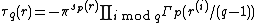
where

where the sum is over roots of 1 in the extension Qp(π)
Gauss sum
In mathematics, a Gauss sum or Gaussian sum is a particular kind of finite sum of roots of unity, typicallyG := G= \sum \chi\cdot \psi...
using a product of values of the p-adic gamma function
P-adic gamma function
In mathematics, the p-adic gamma function Γp is a function of a p-adic variable s analogous to the gamma function. It was first explicitly defined by , though pointed out that implicitly used the same function. defined a p-adic analog Gp of log Γ...
. It is an analog of the Chowla–Selberg formula for the usual gamma function. It implies the Hasse–Davenport relation
Hasse–Davenport relation
The Hasse–Davenport relations, introduced by , are two related identities for Gauss sums, one called the Hasse–Davenport lifting relation, and the other called the Hasse–Davenport product relation. The Hasse–Davenport lifting relation is an equality in number theory relating Gauss sums over...
and generalizes the Stickelberger theorem.
gave another proof of the Gross–Koblitz formula using Dwork's work, and
gave an elementary proof.
Statement
The Gross–Koblitz formula states that the Gauss sum τ can be given in terms of the p-adic gamma function Γp by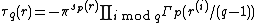
where
- q is a power pf of a prime p
- r is an integer with 0 ≤ r < q–1
- r(i) is the integer whose base p expansion is a cyclic permutation of the first f digits of r.
- sp(r) is the sum of the digits of r in base p
- τ is the Gauss sum

where the sum is over roots of 1 in the extension Qp(π)
- Γp is the p-adic gamma functionP-adic gamma functionIn mathematics, the p-adic gamma function Γp is a function of a p-adic variable s analogous to the gamma function. It was first explicitly defined by , though pointed out that implicitly used the same function. defined a p-adic analog Gp of log Γ...
. - π satisfies πp–1 = –p
- ζπ is the pth root of 1 congruent to 1+π mod π2

