
Hasse–Davenport relation
Encyclopedia
The Hasse–Davenport relations, introduced by , are two related identities for Gauss sums, one called the Hasse–Davenport lifting relation, and the other called the Hasse–Davenport product relation. The Hasse–Davenport lifting relation is an equality in number theory
relating Gauss sum
s over different fields. used it to calculate the zeta function of a Fermat hypersurface over a finite field, which motivated the Weil conjectures
.
Gauss sums are analogues of the gamma function
over finite fields, and the Hasse–Davenport product relation is the analogue of Gauss's multiplication formula
In fact the Hasse–Davenport product relation follows from the analogous multiplication formula for p-adic gamma functions together with the Gross–Koblitz formula
of .
of the vector space Fs over F.
Let be an element of
be an element of  .
.
Let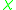 be a multiplicative
be a multiplicative
character
from F to the complex numbers.
Let be the norm from
be the norm from 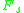 to
to 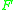 defined by
defined by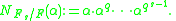
Let
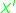 be the multiplicative character on
be the multiplicative character on 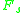 which is the composition of
which is the composition of 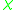 with the norm
with the norm
from Fs to F, that is
Let ψ be some nontrivial additive character of F, and let
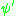 be the additive character on
be the additive character on 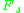 which is the composition of
which is the composition of 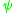 with the trace from Fs to F, that is
with the trace from Fs to F, that is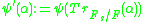
Let
be the Gauss sum
over F, and let
 be the Gauss sum over
be the Gauss sum over 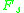 .
.
Then the Hasse–Davenport lifting relation states that
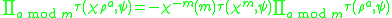
where ρ is a multiplicative character of exact order m dividing q–1 and χ is any multiplicative character and ψ is a non-trivial additive character.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
relating Gauss sum
Gauss sum
In mathematics, a Gauss sum or Gaussian sum is a particular kind of finite sum of roots of unity, typicallyG := G= \sum \chi\cdot \psi...
s over different fields. used it to calculate the zeta function of a Fermat hypersurface over a finite field, which motivated the Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
.
Gauss sums are analogues of the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
over finite fields, and the Hasse–Davenport product relation is the analogue of Gauss's multiplication formula

In fact the Hasse–Davenport product relation follows from the analogous multiplication formula for p-adic gamma functions together with the Gross–Koblitz formula
Gross–Koblitz formula
In mathematics the Gross–Koblitz formula, introduced by expresses a Gauss sum using a product of values of the p-adic gamma function. It is an analog of the Chowla–Selberg formula for the usual gamma function...
of .
Hasse–Davenport lifting relation
Let F be a finite field with q elements, and Fs be the field such that [Fs:F] = s, that is, s is the dimensionDimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of the vector space Fs over F.
Let
 be an element of
be an element of  .
.Let
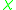 be a multiplicative
be a multiplicativeMultiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
character
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
from F to the complex numbers.
Let
 be the norm from
be the norm from 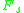 to
to 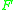 defined by
defined by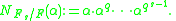
Let
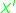 be the multiplicative character on
be the multiplicative character on 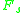 which is the composition of
which is the composition of 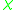 with the norm
with the normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
from Fs to F, that is

Let ψ be some nontrivial additive character of F, and let
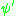 be the additive character on
be the additive character on 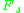 which is the composition of
which is the composition of 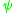 with the trace from Fs to F, that is
with the trace from Fs to F, that is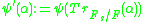
Let

be the Gauss sum
Gauss sum
In mathematics, a Gauss sum or Gaussian sum is a particular kind of finite sum of roots of unity, typicallyG := G= \sum \chi\cdot \psi...
over F, and let
 be the Gauss sum over
be the Gauss sum over 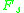 .
.Then the Hasse–Davenport lifting relation states that

Hasse–Davenport product relation
The Hasse–Davenport product relation states that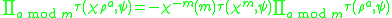
where ρ is a multiplicative character of exact order m dividing q–1 and χ is any multiplicative character and ψ is a non-trivial additive character.

