Hagen-Poiseuille equation
Encyclopedia
In fluid dynamics
, the Hagen–Poiseuille equation is a physical law
that gives the pressure
drop in a fluid flowing through a long cylindrical pipe. The assumptions of the equation are that the flow is laminar viscous and incompressible and the flow is through a constant circular cross-section that is substantially longer than its diameter. The equation is also known as the Hagen–Poiseuille law, Poiseuille law and Poiseuille equation.
The fluid flow will be turbulent
for velocities and pipe diameters above a threshold, leading to larger pressure drops than would be expected according to the Hagen–Poiseuille equation.
or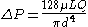
where: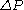
is the pressure drop
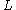is the length of pipe
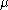is the dynamic viscosity
is the volumetric flow rate
is the radius
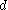is the diameter
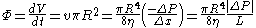
where:
is the volumetric flow rate
is a volume of the liquid poured (cubic meters)
is the time (seconds)
is mean fluid velocity
along the length of the tube (meters/second)
is a distance in direction of flow (meters)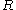
is the internal radius of the tube (meters)
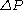is the pressure difference between the two ends (pascals
)
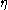is the dynamic fluid viscosity
(pascal
-second
(Pa·s)),
is the total length of the tube in the x direction (meters).
The equation does not hold close to the pipe entrance.
, given a relationship for the friction factor in terms of the Reynolds number:
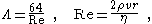
where Re is the Reynolds number and ρ fluid density. In this form the law approximates the Darcy friction factor, the energy (head) loss factor, friction loss factor or Darcy (friction) factor Λ in the laminar flow at very low velocities in cylindrical tube. The theoretical derivation of a slightly different form of the law was made independently by Wiedman in 1856 and Neumann and E. Hagenbach in 1858 (1859, 1860). Hagenbach was the first who called this law the Poiseuille's law.
The law is also very important specially in hemorheology
and hemodynamics
, both fields of physiology
.
The Poiseuilles' law was later in 1891 extended to turbulent flow by L. R. Wilberforce, based on Hagenbach's work.
The derivation of Poiseuille's law is surprisingly simple, but it requires an understanding of viscosity
. When two layers of liquid in contact with each other move at different speeds, there will be a force
between them. This force is proportional
to the area
of contact A, the velocity gradient in the direction of flow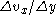
, and a proportionality constant η (viscosity) and is given by
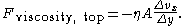
The negative sign is in there because we are concerned with the faster moving liquid (top in figure), which is being slowed by the slower liquid (bottom in figure). By Newton's third law of motion
, the force on the slower liquid is equal and opposite (no negative sign) to the force on the faster liquid. This equation assumes that the area of contact is so large that we can ignore any effects from the edges and that the fluids behave as Newtonian fluid
s.
). To simplify the situation, let's assume that there are a bunch of circular layers (lamina) of liquid, each having a velocity determined only by their radial distance from the center of the tube.
To figure out the motion of the liquid, we need to know all forces acting on each lamina:
The first of these forces comes from the definition of pressure
. The other two forces require us to modify the equations above that we have for viscosity
. In fact, we are not modifying the equations, instead merely plugging in values specific to our problem. Let's focus on the pull from the faster lamina (#2) first.
. From the equation above, we need to know the area
of contact and the velocity gradient
. Think of the lamina as a ring of radius
and thickness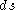 
. The area of contact between the lamina and the faster one is simply the area of the inside of the cylinder: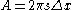 
. We don't know the exact form for the velocity of the liquid within the tube yet, but we do know (from our assumption above) that it is dependent on the radius. Therefore, the velocity gradient is the change of the velocity with respect to the change in the radius
at the intersection of these two laminae. That intersection is at a radius of
. So, considering that this force will be positive with respect to the movement of the liquid (but the derivative of the velocity is negative), the final form of the equation becomes
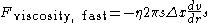
where the vertical bar and subscript s following the derivative
indicates that it should be taken at a radius of
.
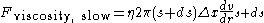
of liquid in the pipe, and by Newton's first law
, there is no net force. If there is no net force then we can add all of the forces together to get zero
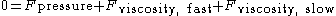
or
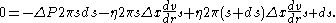
First, to get everything happening at the same point, use the first two terms of a Taylor series expansion
of the velocity gradient:
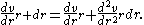
Also, use r instead of s since the lamina was arbitrary and the expression must be valid for all laminae. Grouping like terms and dropping the vertical bar since all derivatives are assumed to be at radius r,
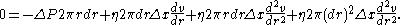
Finally, put this expression in the form of a differential equation
, dropping the term quadratic in dr.
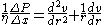
It can be seen that both sides of the equations are negative: there is a drop of pressure along the tube (left side) and both first and second derivatives of the velocity are negative (velocity has a maximum value of the center of the tube). Using the chain rule
, the equation may be re-arranged to:
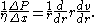
This differential equation is subject to the following boundary conditions:
at 
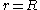-- "no-slip" boundary condition at the wall
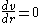at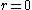 
-- axial symmetry.
Axial symmetry means that the velocity v(r) is maximum at the center of the tube, therefore the first derivative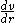
is zero at r = 0.
The differential equation can be integrated to:
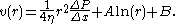
To find A and B, we use the boundary conditions.
First, the symmetry boundary condition indicates:
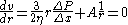at r = 0.
A solution possible only if A = 0. Next the no-slip boundary condition is applied to the remaining equation:
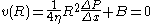
so therefore
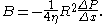
Now we have a formula for the velocity of liquid moving through the tube as a function of the distance from the center of the tube
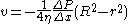
or, at the center of the tube where the liquid is moving fastest (r = 0) with R being the radius of the tube,
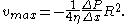
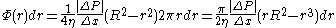
Finally, we integrate
over all lamina via the radius variable r.
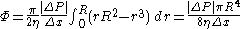
and the linear velocity is not constant along the tube. The flow is usually expressed at outlet pressure. As fluid is compressed or expands, work is done and the fluid is heated and cooled. This means that the flow rate depends on the heat transfer to and from the fluid. For an ideal gas
in the isothermal case, where the temperature of the fluid is permitted to equilibrate with its surroundings, and when the pressure difference between ends of the pipe is small, the volumetric flow rate at the pipe outlet is given by
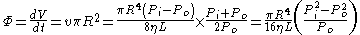
where: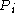
inlet pressure
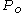outlet pressure
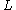is the length of tube
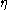is the viscosity
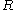is the radius
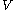is the volume
of the fluid at outlet pressure
is the velocity
of the fluid at outlet pressure
This is usually a good approximation when the flow velocity is less than mach
0.3
This equation can be seen as Poiseuille's law with an extra correction factor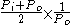
expressing the average pressure relative to the outlet pressure.
is still conceptually useful for understanding circuits. This analogy is also used to study the frequency response of fluid mechanical networks using circuit tools, in which case the fluid network is termed a hydraulic circuit
.
Poiseuille's law corresponds to Ohm's law
for electrical circuits (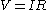
), where the pressure drop 
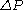is analogous to the voltage
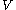and volumetric flow rate 
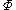is analogous to the current 
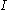. Then the resistance
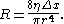
This concept is useful because the effective resistance in a tube is inversely proportional to the fourth power of the radius. This means that halving the radius of the tube increases the resistance to fluid movement by a factor of 16.
Both Ohm's law and Poiseuille's law illustrate transport phenomena
.
(1797-1884) and Jean Louis Marie Poiseuille
.
Poiseuille's law was experimentally derived in 1838 and formulated and published in 1840 and 1846 by Jean Louis Marie Poiseuille
(1797–1869). Hagen did his experiments in 1839.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the Hagen–Poiseuille equation is a physical law
Physical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
that gives the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
drop in a fluid flowing through a long cylindrical pipe. The assumptions of the equation are that the flow is laminar viscous and incompressible and the flow is through a constant circular cross-section that is substantially longer than its diameter. The equation is also known as the Hagen–Poiseuille law, Poiseuille law and Poiseuille equation.
The fluid flow will be turbulent
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
for velocities and pipe diameters above a threshold, leading to larger pressure drops than would be expected according to the Hagen–Poiseuille equation.
Standard fluid dynamics notation
In standard fluid dynamics notation:or
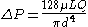
where:
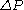is the pressure drop 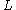is the length of pipe 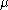is the dynamic viscosity is the volumetric flow rateVolumetric flow rate
The volumetric flow rate in fluid dynamics and hydrometry, is the volume of fluid which passes through a given surface per unit time...
is the radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
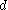is the diameterDiameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
Pi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
is the mathematical constant
Physics notation
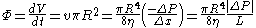
where:
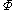is the volumetric flow rate 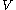is a volume of the liquid poured (cubic meters) is the time (seconds) is mean fluid velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
along the length of the tube (meters/second)
is a distance in direction of flow (meters)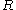 is the internal radius of the tube (meters) 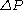is the pressure difference between the two ends (pascalsPascal (unit)
The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...
)
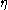is the dynamic fluid viscosityViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
(pascal
Pascal (unit)
The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...
-second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
(Pa·s)),
is the total length of the tube in the x direction (meters).The equation does not hold close to the pipe entrance.
Relation to Darcy–Weisbach
This result is also a solution to the phenomenological Darcy–Weisbach equation in the field of hydraulicsHydraulics
Hydraulics is a topic in applied science and engineering dealing with the mechanical properties of liquids. Fluid mechanics provides the theoretical foundation for hydraulics, which focuses on the engineering uses of fluid properties. In fluid power, hydraulics is used for the generation, control,...
, given a relationship for the friction factor in terms of the Reynolds number:
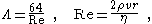
where Re is the Reynolds number and ρ fluid density. In this form the law approximates the Darcy friction factor, the energy (head) loss factor, friction loss factor or Darcy (friction) factor Λ in the laminar flow at very low velocities in cylindrical tube. The theoretical derivation of a slightly different form of the law was made independently by Wiedman in 1856 and Neumann and E. Hagenbach in 1858 (1859, 1860). Hagenbach was the first who called this law the Poiseuille's law.
The law is also very important specially in hemorheology
Hemorheology
Hemorheology is the study of flow properties of blood and its elements...
and hemodynamics
Hemodynamics
Hemodynamics, meaning literally "blood movement" is the study of blood flow or the circulation.All animal cells require oxygen for the conversion of carbohydrates, fats and proteins into carbon dioxide , water and energy in a process known as aerobic respiration...
, both fields of physiology
Physiology
Physiology is the science of the function of living systems. This includes how organisms, organ systems, organs, cells, and bio-molecules carry out the chemical or physical functions that exist in a living system. The highest honor awarded in physiology is the Nobel Prize in Physiology or...
.
The Poiseuilles' law was later in 1891 extended to turbulent flow by L. R. Wilberforce, based on Hagenbach's work.
Derivation
The Hagen–Poiseuille equation can be derived from the Navier–Stokes equations.Viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
. When two layers of liquid in contact with each other move at different speeds, there will be a force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
between them. This force is proportional
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of contact A, the velocity gradient in the direction of flow
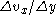, and a proportionality constant η (viscosity) and is given by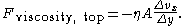The negative sign is in there because we are concerned with the faster moving liquid (top in figure), which is being slowed by the slower liquid (bottom in figure). By Newton's third law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
, the force on the slower liquid is equal and opposite (no negative sign) to the force on the faster liquid. This equation assumes that the area of contact is so large that we can ignore any effects from the edges and that the fluids behave as Newtonian fluid
Newtonian fluid
A Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:...
s.
Liquid flow through a pipe
In a tube we make a basic assumption: the liquid in the center is moving fastest while the liquid touching the walls of the tube is stationary (due to frictionFriction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
). To simplify the situation, let's assume that there are a bunch of circular layers (lamina) of liquid, each having a velocity determined only by their radial distance from the center of the tube.
To figure out the motion of the liquid, we need to know all forces acting on each lamina:
- The force pushing the liquid through the tube is the change in pressure multiplied by the area:
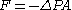. This force is in the direction of the motion of the liquid - the negative sign comes from the conventional way we define 
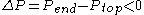. - The pull from the faster lamina immediately closer to the center of the tube
- The drag from the slower lamina immediately closer to the walls of the tube.
The first of these forces comes from the definition of pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
. The other two forces require us to modify the equations above that we have for viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
. In fact, we are not modifying the equations, instead merely plugging in values specific to our problem. Let's focus on the pull from the faster lamina (#2) first.
Faster lamina
Assume that we are figuring out the force on the lamina with radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
. From the equation above, we need to know the areaArea
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of contact and the velocity gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
. Think of the lamina as a ring of radius
and thickness 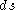. The area of contact between the lamina and the faster one is simply the area of the inside of the cylinder: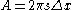 . We don't know the exact form for the velocity of the liquid within the tube yet, but we do know (from our assumption above) that it is dependent on the radius. Therefore, the velocity gradient is the change of the velocity with respect to the change in the radius
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
at the intersection of these two laminae. That intersection is at a radius of
. So, considering that this force will be positive with respect to the movement of the liquid (but the derivative of the velocity is negative), the final form of the equation becomes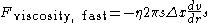where the vertical bar and subscript s following the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
indicates that it should be taken at a radius of
.Slower lamina
Next let's find the force of drag from the slower lamina. We need to calculate the same values that we did for the force from the faster lamina. In this case, the area of contact is at s+ds instead of s. Also, we need to remember that this force opposes the direction of movement of the liquid and will therefore be negative (and that the derivative of the velocity is negative).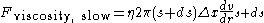Putting it all together
To find the solution for the flow of liquid through a tube, we need to make one last assumption. There is no accelerationAcceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
of liquid in the pipe, and by Newton's first law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
, there is no net force. If there is no net force then we can add all of the forces together to get zero
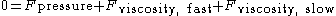
or
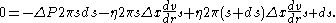
First, to get everything happening at the same point, use the first two terms of a Taylor series expansion
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
of the velocity gradient:
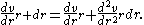
Also, use r instead of s since the lamina was arbitrary and the expression must be valid for all laminae. Grouping like terms and dropping the vertical bar since all derivatives are assumed to be at radius r,
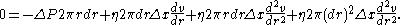
Finally, put this expression in the form of a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
, dropping the term quadratic in dr.
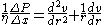
It can be seen that both sides of the equations are negative: there is a drop of pressure along the tube (left side) and both first and second derivatives of the velocity are negative (velocity has a maximum value of the center of the tube). Using the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, the equation may be re-arranged to:
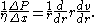
This differential equation is subject to the following boundary conditions:
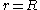at -- "no-slip" boundary condition at the wall 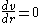at 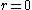-- axial symmetry.Axial symmetry means that the velocity v(r) is maximum at the center of the tube, therefore the first derivative
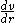is zero at r = 0. The differential equation can be integrated to:
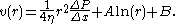
To find A and B, we use the boundary conditions.
First, the symmetry boundary condition indicates:
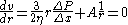at r = 0.A solution possible only if A = 0. Next the no-slip boundary condition is applied to the remaining equation:
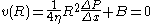
so therefore
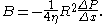
Now we have a formula for the velocity of liquid moving through the tube as a function of the distance from the center of the tube
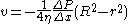
or, at the center of the tube where the liquid is moving fastest (r = 0) with R being the radius of the tube,
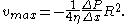
Poiseuille's Law
To get the total volume that flows through the tube, we need to add up the contributions from each lamina. To calculate the flow through each lamina, we multiply the velocity (from above) and the area of the lamina.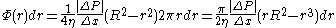Finally, we integrate
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
over all lamina via the radius variable r.
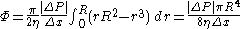
Poiseuille's equation for compressible fluids
For a compressible fluid in a tube the volumetric flow rateVolumetric flow rate
The volumetric flow rate in fluid dynamics and hydrometry, is the volume of fluid which passes through a given surface per unit time...
and the linear velocity is not constant along the tube. The flow is usually expressed at outlet pressure. As fluid is compressed or expands, work is done and the fluid is heated and cooled. This means that the flow rate depends on the heat transfer to and from the fluid. For an ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
in the isothermal case, where the temperature of the fluid is permitted to equilibrate with its surroundings, and when the pressure difference between ends of the pipe is small, the volumetric flow rate at the pipe outlet is given by
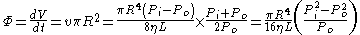
where:
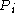inlet pressure 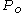outlet pressure 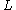is the length of tube 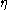is the viscosityViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
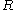is the radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
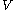is the volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of the fluid at outlet pressure
is the velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the fluid at outlet pressure
This is usually a good approximation when the flow velocity is less than mach
Mach number
Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure...
0.3
This equation can be seen as Poiseuille's law with an extra correction factor
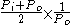expressing the average pressure relative to the outlet pressure.Electrical circuits analogy
Electricity was originally understood to be a kind of fluid. This hydraulic analogyHydraulic analogy
The electronic–hydraulic analogy is the most widely used analogy for "electron fluid" in a metal conductor. Since electric current is invisible and the processes at play in electronics are often difficult to demonstrate, the various electronic components are represented by hydraulic...
is still conceptually useful for understanding circuits. This analogy is also used to study the frequency response of fluid mechanical networks using circuit tools, in which case the fluid network is termed a hydraulic circuit
Hydraulic circuit
A hydraulic circuit is a system comprising an interconnected set of discrete components that transport liquid. The purpose of this system may be to control where fluid flows or to control fluid pressure...
.
Poiseuille's law corresponds to Ohm's law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
for electrical circuits (
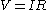), where the pressure drop 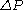is analogous to the voltageVoltage
Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
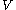and volumetric flow rate 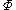is analogous to the current 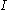. Then the resistanceElectrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
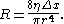
This concept is useful because the effective resistance in a tube is inversely proportional to the fourth power of the radius. This means that halving the radius of the tube increases the resistance to fluid movement by a factor of 16.
Both Ohm's law and Poiseuille's law illustrate transport phenomena
Transport Phenomena
Transport Phenomena is the first textbook that is about transport phenomena. It is specifically designed for chemical engineering students...
.
History
It was developed independently by Gotthilf Heinrich Ludwig HagenGotthilf Heinrich Ludwig Hagen
Gotthilf Heinrich Ludwig Hagen was a German physicist and hydraulic engineer.Hagen was born in Königsberg, East Prussia . He studied mathematics, architecture, and civil engineering at the University of Königsberg...
(1797-1884) and Jean Louis Marie Poiseuille
Jean Louis Marie Poiseuille
Jean Louis Marie Poiseuille was a French physician and physiologist.Poiseuille was born in Paris, France.From 1815 to 1816 he studied at the École Polytechnique in Paris. He was trained in physics and mathematics. In 1828 he earned his D.Sc...
.
Poiseuille's law was experimentally derived in 1838 and formulated and published in 1840 and 1846 by Jean Louis Marie Poiseuille
Jean Louis Marie Poiseuille
Jean Louis Marie Poiseuille was a French physician and physiologist.Poiseuille was born in Paris, France.From 1815 to 1816 he studied at the École Polytechnique in Paris. He was trained in physics and mathematics. In 1828 he earned his D.Sc...
(1797–1869). Hagen did his experiments in 1839.