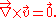Hamiltonian fluid mechanics
Encyclopedia
Hamiltonian fluid mechanics is the application of Hamiltonian
methods to fluid mechanics
. This formalism can only apply to nondissipative fluids.
, inviscid vorticity-free fluid.
Then, the conjugate fields are the mass density field ρ and the velocity potential φ. The Poisson bracket
is given by
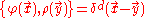
and the Hamiltonian by:
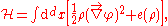
where e is the internal energy
density, as a function of ρ.
For this barotropic flow, the internal energy is related to the pressure p by:
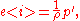
where an apostrophe ('), denotes differentiation with respect to ρ.
This Hamiltonian structure gives rise to the following two equations of motion:
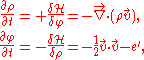
where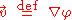
is the velocity and is vorticity-free. The second equation leads to the Euler equations
:
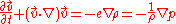
after exploiting the fact that the vorticity is zero:
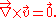
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
methods to fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
. This formalism can only apply to nondissipative fluids.
Irrotational barotropic flow
Take the simple example of a barotropicBarotropic
In meteorology, a barotropic atmosphere is one in which the pressure depends only on the density and vice versa, so that isobaric surfaces are also isopycnic surfaces . The isobaric surfaces will also be isothermal surfaces, hence the geostrophic wind is independent of height...
, inviscid vorticity-free fluid.
Then, the conjugate fields are the mass density field ρ and the velocity potential φ. The Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
is given by
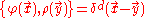
and the Hamiltonian by:
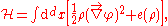
where e is the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
density, as a function of ρ.
For this barotropic flow, the internal energy is related to the pressure p by:
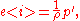
where an apostrophe ('), denotes differentiation with respect to ρ.
This Hamiltonian structure gives rise to the following two equations of motion:
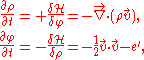
where
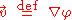is the velocity and is vorticity-free. The second equation leads to the Euler equationsEuler equations
In fluid dynamics, the Euler equations are a set of equations governing inviscid flow. They are named after Leonhard Euler. The equations represent conservation of mass , momentum, and energy, corresponding to the Navier–Stokes equations with zero viscosity and heat conduction terms. Historically,...
:
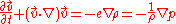
after exploiting the fact that the vorticity is zero: