
Hamiltonian lattice gauge theory
Encyclopedia
In physics
, Hamiltonian lattice gauge theory is a calculational approach to gauge theory
and a special case of lattice gauge theory
in which the space is discretized but time is not. The Hamiltonian
is then re-expressed as a function of degrees of freedom defined on a d-dimensional lattice.
Following Wilson, the spatial components of the vector potential
are replaced with Wilson lines over the edges, but the time component is associated with the vertices. However, the temporal gauge is often employed, setting the electric potential
to zero. The eigenvalues of the Wilson line operators U(e) (where e is the (oriented) edge in question) take on values on the Lie group
G. It is assumed that G is compact
, otherwise we run into many problems. The conjugate operator to U(e) is the electric field
E(e) whose eigenvalues take on values in the Lie algebra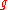 . The Hamiltonian receives contributions coming from the plaquettes (the magnetic contribution) and contributions coming from the edges (the electric contribution).
. The Hamiltonian receives contributions coming from the plaquettes (the magnetic contribution) and contributions coming from the edges (the electric contribution).
Hamiltonian lattice gauge theory is exactly dual to a theory of spin network
s. This involves using the Peter-Weyl theorem. In the spin network basis, the spin network states are eigenstates of the operator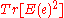 .
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Hamiltonian lattice gauge theory is a calculational approach to gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
and a special case of lattice gauge theory
Lattice gauge theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice. Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum electrodynamics, quantum chromodynamics and the Standard...
in which the space is discretized but time is not. The Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
is then re-expressed as a function of degrees of freedom defined on a d-dimensional lattice.
Following Wilson, the spatial components of the vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
are replaced with Wilson lines over the edges, but the time component is associated with the vertices. However, the temporal gauge is often employed, setting the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
to zero. The eigenvalues of the Wilson line operators U(e) (where e is the (oriented) edge in question) take on values on the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G. It is assumed that G is compact
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
, otherwise we run into many problems. The conjugate operator to U(e) is the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
E(e) whose eigenvalues take on values in the Lie algebra
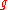 . The Hamiltonian receives contributions coming from the plaquettes (the magnetic contribution) and contributions coming from the edges (the electric contribution).
. The Hamiltonian receives contributions coming from the plaquettes (the magnetic contribution) and contributions coming from the edges (the electric contribution).Hamiltonian lattice gauge theory is exactly dual to a theory of spin network
Spin network
In physics, a spin network is a type of diagram which can be used to represent states and interactions between particles and fields in quantum mechanics. From a mathematical perspective, the diagrams are a concise way to represent multilinear functions and functions between representations of...
s. This involves using the Peter-Weyl theorem. In the spin network basis, the spin network states are eigenstates of the operator
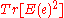 .
.

