Hamming scheme
Encyclopedia
The Hamming scheme, named after Richard Hamming
, is also known as the hyper-cubic association scheme, and it is the most important example for coding theory
. In this scheme
, the set of binary vectors of length 
, and two vectors 
, 
are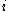 
-th associates if they have Hamming distance
apart.
Recall that an association scheme
is visualized as a complete graph
with labeled edges. The graph has
vertices, one for each point of 
, and the edge joining vertices 
and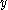 
is labeled 
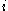if 
and 
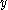are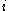 
-th associates. Each edge has a unique label, and the number of triangles with a fixed base labeled 
having the other edges labele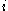d 
and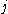 
is a constant 
, depending on 
but not on the choice of the base. In particular, each vertex is incident with exactly 
edges labeled 
; 
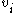is the valency of the relation
.
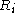The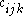
in a Hamming scheme are given by
Richard Hamming
Richard Wesley Hamming was an American mathematician whose work had many implications for computer science and telecommunications...
, is also known as the hyper-cubic association scheme, and it is the most important example for coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
. In this scheme
, the set of binary vectors of length , and two vectors , are 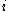-th associates if they have Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
apart.Recall that an association scheme
Association scheme
The theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
is visualized as a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
with labeled edges. The graph has
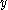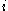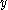vertices, one for each point of , and the edge joining vertices and is labeled if and are 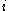-th associates. Each edge has a unique label, and the number of triangles with a fixed base labeled having the other edges labele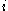d and 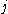is a constant , depending on but not on the choice of the base. In particular, each vertex is incident with exactly edges labeled ; 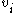is the valency of the relationRelation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
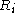.The
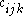in a Hamming scheme are given by-
Here,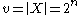
and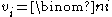 
. The matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
in the Bose-Mesner algebraBose–Mesner algebraIn mathematics, a Bose–Mesner algebra is a set of matrices, together with set of rules for combining those matrices, such that certain conditions apply...
are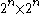
matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, with rows and columns labeled by vectors
. In particular the 
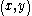-th entry of 
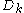is 
if and only if
.
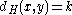