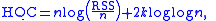Hannan-Quinn information criterion
Encyclopedia
In statistics
, the Hannan-Quinn information criterion (HQC) is a criterion for model selection
. It is an alternative to Akaike information criterion
(AIC) and Bayesian information criterion (BIC). It is given as
where k is the number of parameters, n is the number of observations, and RSS is the residual sum of squares
that results from linear regression
or other statistical model.
Burnham & Anderson (2002) say that HQC, "while often cited, seems to have seen little use in practice" (p. 287). They also note that HQC, like BIC, but unlike AIC, is not an estimator of Kullback–Leibler divergence
. Claeskens & Hjort (2008) note that QHC, like BIC, but unlike AIC, is not asymptotically efficient
(Ch. 4), and further point out that whatever method is being used for fine-tuning the criterion will be more important in practice than the term log log n, since this latter number is small even for very large n.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Hannan-Quinn information criterion (HQC) is a criterion for model selection
Model selection
Model selection is the task of selecting a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered...
. It is an alternative to Akaike information criterion
Akaike information criterion
The Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
(AIC) and Bayesian information criterion (BIC). It is given as
where k is the number of parameters, n is the number of observations, and RSS is the residual sum of squares
Residual sum of squares
In statistics, the residual sum of squares is the sum of squares of residuals. It is also known as the sum of squared residuals or the sum of squared errors of prediction . It is a measure of the discrepancy between the data and an estimation model...
that results from linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
or other statistical model.
Burnham & Anderson (2002) say that HQC, "while often cited, seems to have seen little use in practice" (p. 287). They also note that HQC, like BIC, but unlike AIC, is not an estimator of Kullback–Leibler divergence
Kullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
. Claeskens & Hjort (2008) note that QHC, like BIC, but unlike AIC, is not asymptotically efficient
Efficiency (statistics)
In statistics, an efficient estimator is an estimator that estimates the quantity of interest in some “best possible” manner. The notion of “best possible” relies upon the choice of a particular loss function — the function which quantifies the relative degree of undesirability of estimation errors...
(Ch. 4), and further point out that whatever method is being used for fine-tuning the criterion will be more important in practice than the term log log n, since this latter number is small even for very large n.