Hartogs' theorem
Encyclopedia
In mathematics
, Hartogs' theorem is a fundamental result of Friedrich Hartogs
in the theory of several complex variables
. Roughly speaking, it states that a 'separately analytic' function is continuous. More precisely, if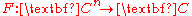
is an analytic function
in each variable zi, 1 ≤ i ≤ n, while the other variables are held constant, then F is a continuous function
.
A corollary
of this is that F is then in fact an analytic function in the n-variable sense (i.e. that locally it has a Taylor expansion). Therefore 'separate analyticity' and 'analyticity' are coincident notions, in the several complex variables theory.
Note that there is no analogue of this theorem
for real
variables. If we assume that a function
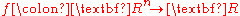
is differentiable (or even analytic
) in each variable separately, it is not true that
will necessarily be continuous. A counterexample in two dimensions is given by
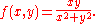
This function has well-defined partial derivative
s in
and 
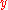at 0, but it is not continuous
at 0 (the limits
along the lines
and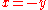 
give different results).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Hartogs' theorem is a fundamental result of Friedrich Hartogs
Friedrich Hartogs
Friedrich Moritz Hartogs was a German-Jewish mathematician, known for work on set theory and foundational results on several complex variables.- See also :*Hartogs domain*Hartogs–Laurent expansion...
in the theory of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. Roughly speaking, it states that a 'separately analytic' function is continuous. More precisely, if
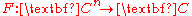is an analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
in each variable zi, 1 ≤ i ≤ n, while the other variables are held constant, then F is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
.
A corollary
Corollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
of this is that F is then in fact an analytic function in the n-variable sense (i.e. that locally it has a Taylor expansion). Therefore 'separate analyticity' and 'analyticity' are coincident notions, in the several complex variables theory.
Note that there is no analogue of this theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
for real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
variables. If we assume that a function
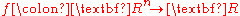
is differentiable (or even analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
) in each variable separately, it is not true that
will necessarily be continuous. A counterexample in two dimensions is given by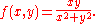This function has well-defined partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s in
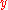and at 0, but it is not continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
at 0 (the limits
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
along the lines
and 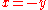give different results).