Hartogs–Rosenthal theorem
Encyclopedia
In mathematics
, the Hartogs–Rosenthal theorem is a classical result in complex analysis
on the uniform approximation of continuous functions on compact subsets of the complex plane
by rational function
s. The theorem was proved in 1931 by the German mathematicians Friedrich Hartogs
and Arthur Rosenthal
and has been widely applied, particularly in operator theory
.
zero, then any continuous complex-valued function on K can be uniformly approximated by rational functions.
and 
.
So it suffices to show that
can be uniformly approximated by a rational function on K.
Let g(z) be a smooth function
of compact support on C equal to 1 on K and set
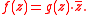
By the generalized Cauchy integral formula
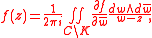
since K has measure zero.
Restricting z to K and taking Riemann approximating sums
for the integral on the right hand side yields the required uniform approximation of
by a rational function.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hartogs–Rosenthal theorem is a classical result in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
on the uniform approximation of continuous functions on compact subsets of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
by rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s. The theorem was proved in 1931 by the German mathematicians Friedrich Hartogs
Friedrich Hartogs
Friedrich Moritz Hartogs was a German-Jewish mathematician, known for work on set theory and foundational results on several complex variables.- See also :*Hartogs domain*Hartogs–Laurent expansion...
and Arthur Rosenthal
Arthur Rosenthal
Arthur Rosenthal was a German mathematician.-Career:Rosenthal's mathematical studies started in 1905 in Munich, under Ferdinand Lindemann and Arnold Sommerfeld at the University of Munich and the Technical University Munich, as well as at the University of Göttingen...
and has been widely applied, particularly in operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
.
Statement of theorem
The Hartogs–Rosenthal theorem states that if K is a compact subset of the complex plane with Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero, then any continuous complex-valued function on K can be uniformly approximated by rational functions.
Proof of theorem
By the Stone–Weierstrass theorem any complex-valued continuous function on K can be uniformly approximated by a polynomial in and .So it suffices to show that
can be uniformly approximated by a rational function on K.Let g(z) be a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
of compact support on C equal to 1 on K and set
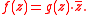
By the generalized Cauchy integral formula
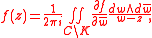
since K has measure zero.
Restricting z to K and taking Riemann approximating sums
Riemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
for the integral on the right hand side yields the required uniform approximation of
by a rational function.