Henry John Stephen Smith
Encyclopedia
Henry John Stephen Smith (2 November 1826 Dublin, Ireland
– 9 February 1883 Oxford
, Oxfordshire
, England
) was a mathematician
remembered for his work in elementary divisors, quadratic form
s, and Smith–Minkowski–Siegel mass formula
in number theory
. In matrix theory he is visible today in having his name on the Smith Normal Form
of a matrix
.
, who died when Henry was two. His mother very soon afterward moved the family to England. He lived in several places in England as a boy, and had private tutors for his education. His mother did not send him to school but educated him herself until age 6, at which point she hired private tutors. At age 15 Smith was admitted in 1841 to Rugby School
in Warwickshire
, where Thomas Arnold
was the school's headmaster. This came about because his tutor Henry Highton
took up a housemaster position there.
At 19 he won an entrance scholarship to Balliol College, Oxford
. He graduated aged 8 in 1849 with high honours in both mathematics and classics. Smith was fluent in French having spent holidays in France, and he took classes in mathematics at the Sorbonne
in Paris during the 1846-1847 academic year.
On account of his ability as a man of affairs, Smith was in demand for academic administrative and committee work: He was Keeper of the Oxford University Museum; a Mathematical Examiner for the University of London; a member of a Royal Commission to review scientific education practice; a member of the commission to reform University of Oxford governance; chairman of the committee of scientists overseeing the Meteorological Office; twice president of the London Mathematical Society; etc.
His two earliest mathematical papers were on geometrical subjects, but the third concerned the theory of numbers. Following the example of Gauss, he wrote his first paper on the theory of numbers in Latin: "De compositione numerorum primorum formæ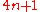
ex duobus quadratis." In it he proves in an original manner the theorem of Fermat---"That every prime number of the form 
(
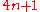being an integer) is the sum of two square numbers." In his second paper he gives an introduction to the theory of numbers.
In 1858 he was selected by the British Association to prepare a report upon the Theory of Numbers. It was prepared in five parts, extending over the years 1859-1865. It is neither a history nor a treatise, but something intermediate. The author analyzes with remarkable clearness and order the works of mathematicians for the preceding century upon the theory of congruences, and upon that of binary quadratic forms. He returns to the original sources, indicates the principle and sketches the course of the demonstrations, and states the result, often adding something of his own.
During the preparation of the Report, and as a logical consequence of the researches connected therewith, Smith published several original contributions to the higher arithmetic. Some were in complete form and appeared in the Philosophical Transactions of the Royal Society of London; others were incomplete, giving only the results without the extended demonstrations, and appeared in the Proceedings of that Society. One of the latter, entitled "On the orders and genera of quadratic forms containing more than three indeterminates," enunciates certain general principles by means of which he solves a problem proposed by Eisenstein, namely, the decomposition of integer numbers into the sum of five squares; and further, the analogous problem for seven squares. It was also indicated that the four, six, and eight-square theorems of Jacobi, Eisenstein and Lionville were deducible from the principles set forth.
In 1868 he returned to the geometrical researches which had first occupied his attention. For a memoir on "Certain cubic and biquadratic problems" the Royal Academy of Sciences of Berlin awarded him the Steiner prize.
In February, 1882, he was surprised to see in the Comptes rendus that the subject proposed by the Paris Academy of Science
for the Grand prix des sciences mathématiques was the theory of the decomposition of integer numbers into a sum of five squares; and that the attention of competitors was directed to the results announced without demonstration by Eisenstein, whereas nothing was said about his papers dealing with the same subject in the Proceedings of the Royal Society. He wrote to M. Hermite calling his attention to what he had published; in reply he was assured that the members of the commission did not know of the existence of his papers, and he was advised to complete his demonstrations and submit the memoir according to the rules of the competition. According to the rules each manuscript bears a motto, and the corresponding envelope containing the name of the successful author is opened. There were still three months before the closing of the concours (1 June 1882) and Smith set to work, prepared the memoir and despatched it in time.
Two months after his death the Paris Academy made their award. Two of the three memoirs sent in were judged worthy of the prize. When
the envelopes were opened, the authors were found to be Smith and Minkowski
, a young mathematician of Koenigsberg, Prussia. No notice was taken of Smith's previous publication on the subject, and M. Hermite on being written to, said that he forgot to bring the matter to the notice of the commission.
Ireland
Ireland is an island to the northwest of continental Europe. It is the third-largest island in Europe and the twentieth-largest island on Earth...
– 9 February 1883 Oxford
Oxford
The city of Oxford is the county town of Oxfordshire, England. The city, made prominent by its medieval university, has a population of just under 165,000, with 153,900 living within the district boundary. It lies about 50 miles north-west of London. The rivers Cherwell and Thames run through...
, Oxfordshire
Oxfordshire
Oxfordshire is a county in the South East region of England, bordering on Warwickshire and Northamptonshire , Buckinghamshire , Berkshire , Wiltshire and Gloucestershire ....
, England
England
England is a country that is part of the United Kingdom. It shares land borders with Scotland to the north and Wales to the west; the Irish Sea is to the north west, the Celtic Sea to the south west, with the North Sea to the east and the English Channel to the south separating it from continental...
) was a mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
remembered for his work in elementary divisors, quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s, and Smith–Minkowski–Siegel mass formula
Smith–Minkowski–Siegel mass formula
In mathematics, the Smith–Minkowski–Siegel mass formula is a formula for the sum of the weights of the lattices in a genus, weighted by the reciprocals of the orders of their automorphism groups...
in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. In matrix theory he is visible today in having his name on the Smith Normal Form
Smith normal form
In mathematics, the Smith normal form is a normal form that can be defined for any matrix with entries in a principal ideal domain . The Smith normal form of a matrix is diagonal, and can be obtained from the original matrix by multiplying on the left and right by invertible square matrices...
of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
Education
He was born in Dublin, Ireland, the fourth child of John Smith, a barristerBarrister
A barrister is a member of one of the two classes of lawyer found in many common law jurisdictions with split legal professions. Barristers specialise in courtroom advocacy, drafting legal pleadings and giving expert legal opinions...
, who died when Henry was two. His mother very soon afterward moved the family to England. He lived in several places in England as a boy, and had private tutors for his education. His mother did not send him to school but educated him herself until age 6, at which point she hired private tutors. At age 15 Smith was admitted in 1841 to Rugby School
Rugby School
Rugby School is a co-educational day and boarding school located in the town of Rugby, Warwickshire, England. It is one of the oldest independent schools in Britain.-History:...
in Warwickshire
Warwickshire
Warwickshire is a landlocked non-metropolitan county in the West Midlands region of England. The county town is Warwick, although the largest town is Nuneaton. The county is famous for being the birthplace of William Shakespeare...
, where Thomas Arnold
Thomas Arnold
Dr Thomas Arnold was a British educator and historian. Arnold was an early supporter of the Broad Church Anglican movement...
was the school's headmaster. This came about because his tutor Henry Highton
Henry Highton
Henry Highton was an English schoolmaster and clergyman, Principal of Cheltenham College, known also as a scientific and theological writer.-Life:...
took up a housemaster position there.
At 19 he won an entrance scholarship to Balliol College, Oxford
Balliol College, Oxford
Balliol College , founded in 1263, is one of the constituent colleges of the University of Oxford in England but founded by a family with strong Scottish connections....
. He graduated aged 8 in 1849 with high honours in both mathematics and classics. Smith was fluent in French having spent holidays in France, and he took classes in mathematics at the Sorbonne
Collège de Sorbonne
The Collège de Sorbonne was a theological college of the University of Paris, founded in 1257 by Robert de Sorbon, after whom it is named. With the rest of the Paris colleges, it was suppressed during the French Revolution. It was restored in 1808 but finally closed in 1882. The name Sorbonne...
in Paris during the 1846-1847 academic year.
Academic career
Smith remained at Balliol as a mathematics tutor following his graduation in 1849 and was soon promoted to Fellow status. In 1861 he was promoted to the Savilian Chair of Geometry at Oxford. In 1873 he was made the beneficiary of a fellowship at Corpus Christi College, Oxford, and gave up teaching at Balliol.On account of his ability as a man of affairs, Smith was in demand for academic administrative and committee work: He was Keeper of the Oxford University Museum; a Mathematical Examiner for the University of London; a member of a Royal Commission to review scientific education practice; a member of the commission to reform University of Oxford governance; chairman of the committee of scientists overseeing the Meteorological Office; twice president of the London Mathematical Society; etc.
Publications in number theory
An overview of Smith's mathematics contained in a lengthy obituary published in a professional journal in 1884 is reproduced at NumberTheory.Org http://www.numbertheory.org/obituaries/OTHERS/smith/page4.html. The following is an extract from it.His two earliest mathematical papers were on geometrical subjects, but the third concerned the theory of numbers. Following the example of Gauss, he wrote his first paper on the theory of numbers in Latin: "De compositione numerorum primorum formæ
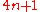ex duobus quadratis." In it he proves in an original manner the theorem of Fermat---"That every prime number of the form 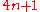( being an integer) is the sum of two square numbers." In his second paper he gives an introduction to the theory of numbers.In 1858 he was selected by the British Association to prepare a report upon the Theory of Numbers. It was prepared in five parts, extending over the years 1859-1865. It is neither a history nor a treatise, but something intermediate. The author analyzes with remarkable clearness and order the works of mathematicians for the preceding century upon the theory of congruences, and upon that of binary quadratic forms. He returns to the original sources, indicates the principle and sketches the course of the demonstrations, and states the result, often adding something of his own.
During the preparation of the Report, and as a logical consequence of the researches connected therewith, Smith published several original contributions to the higher arithmetic. Some were in complete form and appeared in the Philosophical Transactions of the Royal Society of London; others were incomplete, giving only the results without the extended demonstrations, and appeared in the Proceedings of that Society. One of the latter, entitled "On the orders and genera of quadratic forms containing more than three indeterminates," enunciates certain general principles by means of which he solves a problem proposed by Eisenstein, namely, the decomposition of integer numbers into the sum of five squares; and further, the analogous problem for seven squares. It was also indicated that the four, six, and eight-square theorems of Jacobi, Eisenstein and Lionville were deducible from the principles set forth.
In 1868 he returned to the geometrical researches which had first occupied his attention. For a memoir on "Certain cubic and biquadratic problems" the Royal Academy of Sciences of Berlin awarded him the Steiner prize.
In February, 1882, he was surprised to see in the Comptes rendus that the subject proposed by the Paris Academy of Science
for the Grand prix des sciences mathématiques was the theory of the decomposition of integer numbers into a sum of five squares; and that the attention of competitors was directed to the results announced without demonstration by Eisenstein, whereas nothing was said about his papers dealing with the same subject in the Proceedings of the Royal Society. He wrote to M. Hermite calling his attention to what he had published; in reply he was assured that the members of the commission did not know of the existence of his papers, and he was advised to complete his demonstrations and submit the memoir according to the rules of the competition. According to the rules each manuscript bears a motto, and the corresponding envelope containing the name of the successful author is opened. There were still three months before the closing of the concours (1 June 1882) and Smith set to work, prepared the memoir and despatched it in time.
Two months after his death the Paris Academy made their award. Two of the three memoirs sent in were judged worthy of the prize. When
the envelopes were opened, the authors were found to be Smith and Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
, a young mathematician of Koenigsberg, Prussia. No notice was taken of Smith's previous publication on the subject, and M. Hermite on being written to, said that he forgot to bring the matter to the notice of the commission.
External links
- Henry John Stephen Smith at WikiquoteWikiquoteWikiquote is one of a family of wiki-based projects run by the Wikimedia Foundation, running on MediaWiki software. Based on an idea by Daniel Alston and implemented by Brion Vibber, the goal of the project is to produce collaboratively a vast reference of quotations from prominent people, books,...