
Herman ring
Encyclopedia
In the mathematical discipline known as complex dynamics
for rational function
s, the Herman ring is a Fatou component
. where the rational function is conformally conjugate to a irrational rotation of the standard annulus
.
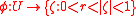
and an irrational number
 , such that
, such that

So the dynamics on the Herman ring is simple.
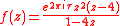
where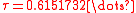 such that the rotation number
such that the rotation number
of ƒ on the
unit circle is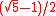 .
.
The picture shown on the right is the Julia set of ƒ: the curves in the white annulus are the orbits of some points under the iterations of ƒ while the dashed line denotes the unit circle.
There is an example of rational function that possesses a Herman ring, and some periodic parabolic Fatou components (see Classification of Fatou components
) at the same time.
Further, there is a rational function which possesses a Herman ring with period 2.
Here the expression of this rational function is
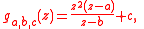
where
Complex dynamics
Complex dynamics is the study of dynamical systems defined by iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions.-Techniques:*General** Montel's theorem...
for rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s, the Herman ring is a Fatou component
Classification of Fatou components
In mathematics, if f = P/Q is a rational function defined in the extended complex plane, and ifthen for a periodic component U of the Fatou set, exactly one of the following holds:# U contains an attracting periodic point# U is parabolic...
. where the rational function is conformally conjugate to a irrational rotation of the standard annulus
Annulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
.
Formal definition
Namely if ƒ possesses a Herman ring U with period p, then there exists a conformal mapping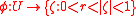
and an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
 , such that
, such that
So the dynamics on the Herman ring is simple.
Name
It was introduced by, and later named after, who first found and constructed this type of Fatou component.Examples
Here is an example of a rational function which possesses a Herman ring.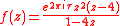
where
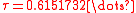 such that the rotation number
such that the rotation numberRotation number
In mathematics, the rotation number is an invariant of homeomorphisms of the circle. It was first defined by Henri Poincaré in 1885, in relation to the precession of the perihelion of a planetary orbit...
of ƒ on the
unit circle is
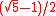 .
.The picture shown on the right is the Julia set of ƒ: the curves in the white annulus are the orbits of some points under the iterations of ƒ while the dashed line denotes the unit circle.
There is an example of rational function that possesses a Herman ring, and some periodic parabolic Fatou components (see Classification of Fatou components
Classification of Fatou components
In mathematics, if f = P/Q is a rational function defined in the extended complex plane, and ifthen for a periodic component U of the Fatou set, exactly one of the following holds:# U contains an attracting periodic point# U is parabolic...
) at the same time.
Further, there is a rational function which possesses a Herman ring with period 2.
Here the expression of this rational function is
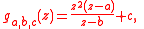
where
-
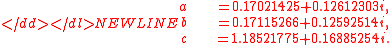
This example was constructed by quasiconformal surgery
from the quadratic polynomial
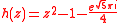
which possesses a Siegel disk with period 2. The parameters a, b, c are calculated by trial and errorTrial and errorTrial and error, or trial by error, is a general method of problem solving, fixing things, or for obtaining knowledge."Learning doesn't happen from failure itself but rather from analyzing the failure, making a change, and then trying again."...
.
Letting
-

then the period of one of the Herman ring of ga,b,c is 3.
ShishikuraMitsuhiro Shishikurais a Japanese mathematician working in the field of complex dynamics. He is currently professor at Kyoto University in Japan.Shishikura became internationally recognized for two of his earliest contributions, both of which solved long-standing open problems....
also given an example: a rational function which possesses a Herman ring with period 2, but the parameters showed above are different from his.
So there is a question: How to find the formulas of the rational functions which possess Herman rings with higher period?
According to the result of Shishikura, if a rational function ƒ possesses a Herman ring, then the degree of ƒ is at least 3. There also exist meromorphic functionMeromorphic functionIn complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s that possess Herman rings.
-

