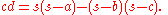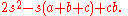Heron's formula
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Heron's (or Hero's) formula, named after Heron of Alexandria, states that the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
T of a triangle
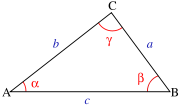
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
whose sides have lengths a, b, and c is
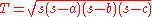
where s is the semiperimeter
Semiperimeter
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name...
of the triangle:
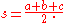
Heron's formula can also be written as:
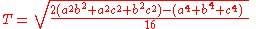
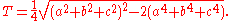
Heron's formula is distinguished from other formulas for the area of a triangle, such as half the base times the height or half the modulus of a cross product of two sides, by requiring no arbitrary choice of side as base or vertex as origin.
History
The formula is credited to Heron (or Hero) of Alexandria, and a proof can be found in his book, Metrica, written c. A.D. 60. It has been suggested that ArchimedesArchimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
knew the formula, and since Metrica is a collection of the mathematical knowledge available in the ancient world, it is possible that it predates the reference given in the work.
A formula equivalent to Heron's namely:
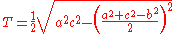, where 
was discovered by the Chinese independently of the Greeks. It was published in Shushu Jiuzhang (“Mathematical Treatise in Nine Sections
Mathematical Treatise in Nine Sections
The Mathematical Treatise in Nine Sections is a mathematical text written by Chinese Southern Song dynasty mathematician Qin Jiushao in the year 1247.This book contains nine chapters:#Da Yan type ;#Heaven phenomena...
”), written by Qin Jiushao and published in A.D. 1247.
Proof
A modern proof, which uses algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and is quite unlike the one provided by Heron (in his book Metrica), follows. Let a, b, c be the sides of the triangle and A, B, C the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s opposite those sides. We have
by the law of cosines
Law of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
. From this proof get the algebraic statement:
The altitude
Altitude (triangle)
In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...
of the triangle on base a has length b·sin(C), and it follows
-
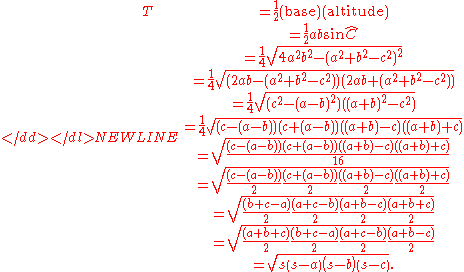
The difference of two squaresDifference of two squaresIn mathematics, the difference of two squares, or the difference of perfect squares, is when a number is squared, or multiplied by itself, and is then subtracted from another squared number...
factorization was used in two different steps.
Proof using the Pythagorean theorem
Heron's original proof made use of cyclic quadrilateral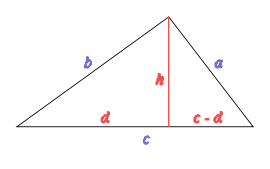
Cyclic quadrilateralIn Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
s, while other arguments appeal to trigonometryTrigonometryTrigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
as above, or to the incenter and one excircle of the triangle http://www.math.dartmouth.edu/~doyle/docs/heron/heron.txt. The following argument reduces Heron's formula directly to the Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
using only elementary means.
In the form 4T 2 = 4s(s − a)(s − b)(s − c), Heron's formula reduces on the left to (ch)2, or
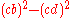which is the same as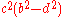 
using b 2 − d 2 = h 2 by the Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, and on the right to
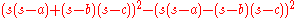
via the identity (p + q) 2 − (p − q) 2 = 4pq. It therefore suffices to show
and
Then expanding the former you get the following:
and that reduces to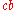
by substituting 2s = (a + b + c) and simplifying. Submitting for s the latter s(s − a) − (s − b)(s − c) reduces only as far as (b 2 + c 2 − a 2)/2. But if we replace b 2 by d 2 + h 2 and a 2 by (c − d) 2 + h 2, both by Pythagoras, simplification then produces cd as required.
Generalizations
Heron's formula is a special case of Brahmagupta's formulaBrahmagupta's formulaIn Euclidean geometry, Brahmagupta's formula finds the area of any quadrilateral given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle.- Basic form :...
for the area of a cyclic quadrilateralCyclic quadrilateralIn Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
. Heron's formula and Brahmagupta's formula are both special cases of Bretschneider's formula for the area of a quadrilateralQuadrilateralIn Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
. Heron's formula can be obtained from Brahmagupta's formula or Bretschneider's formula by setting one of the sides of the quadrilateral to zero.
Heron's formula is also a special case of the formula of the area of the trapezoidTrapezoidIn Euclidean geometry, a convex quadrilateral with one pair of parallel sides is referred to as a trapezoid in American English and as a trapezium in English outside North America. A trapezoid with vertices ABCD is denoted...
based only on its sides. Heron's formula is obtained by setting the smaller parallel side to zero.
Expressing Heron's formula with a Cayley–Menger determinant in terms of the squares of the distanceDistanceDistance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
s between the three given vertices,
illustrates its similarity to Tartaglia's formula for the volumeVolumeVolume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a three-simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
.
Another generalization of Heron's formula to polygons inscribed in a circle was discovered by David P. RobbinsDavid P. RobbinsDavid P. Robbins was an American mathematician. He is most famous for introducing alternating sign matrices and his work on generalized Heron's formula....
.
Heron-looking formula for tetrahedron
If U, V, W, u, v, w are lengths of edges of the tetrahedron (first three form a triangle; u opposite to U and so on), then
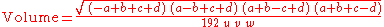
where
-
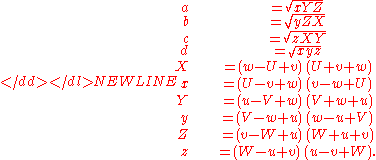
External links
- A Proof of the Pythagorean Theorem From Heron's Formula at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Interactive applet and area calculator using Heron's Formula
- J.H. Conway discussion on Heron's Formula
- A Geometric Proof of Heron's Formula
- A Proof of the Pythagorean Theorem From Heron's Formula at cut-the-knot
-
