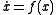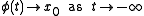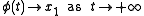Heteroclinic orbit
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the phase portrait
Phase portrait
A phase portrait is a geometric representation of the trajectories of a dynamical system in the phase plane. Each set of initial conditions is representated by a different curve, or point....
of a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
, a heteroclinic orbit (sometimes called a heteroclinic connection) is a path in phase space which joins two different equilibrium points. If the equilibrium points at the start and end of the orbit are the same, the orbit is a homoclinic orbit
Homoclinic orbit
In mathematics, a homoclinic orbit is a trajectory of a flow of a dynamical system which joins a saddle equilibrium point to itself. More precisely, a homoclinic orbit lies in the intersection of the stable manifold and the unstable manifold of an equilibrium.Homoclinic orbits and homoclinic points...
.
Consider the continuous dynamical system described by the ODE
Suppose there are equilibria at
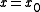and 
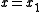, then a solution 
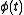is a heteroclinic orbit from 
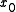to 
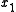if
and
This implies that the orbit is contained in the stable manifold
Stable manifold
In mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...
of
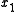and the unstable manifold of 
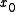.Symbolic dynamics
By using the Markov partitionMarkov partition
A Markov partition is a tool used in dynamical systems theory, allowing the methods of symbolic dynamics to be applied to the study of hyperbolic systems. By using a Markov partition, the system can be made to resemble a discrete-time Markov process, with the long-term dynamical characteristics...
, the long-time behaviour of hyperbolic system can be studied using the techniques of symbolic dynamics
Symbolic dynamics
In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
. In this case, a heteroclinic orbit has a particularly simple and clear representation. Suppose that
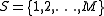is a finite set of M symbols. The dynamics of a point x is then represented by a bi-infinite string of symbols
A periodic point
Periodic point
In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...
of the system is simply a recurring sequence of letters. A heteroclinic orbit is then the joining of two distinct periodic orbits. It may be written as
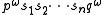
where
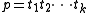is a sequence of symbols of length k, (of course, 
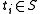), and 
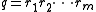is another sequence of symbols, of length m (likewise, 
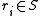). The notation 
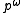simply denotes the repetition of p an infinite number of times. Thus, a heteroclinic orbit can be understood as the transition from one periodic orbit to another. By contrast, a homoclinic orbitHomoclinic orbit
In mathematics, a homoclinic orbit is a trajectory of a flow of a dynamical system which joins a saddle equilibrium point to itself. More precisely, a homoclinic orbit lies in the intersection of the stable manifold and the unstable manifold of an equilibrium.Homoclinic orbits and homoclinic points...
can be written as
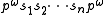
with the intermediate sequence
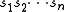being non-empty, and, of course, not being p, as otherwise, the orbit would simply be 
.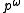