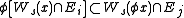Markov partition
Encyclopedia
A Markov partition is a tool used in dynamical systems theory, allowing the methods of symbolic dynamics
to be applied to the study of hyperbolic systems. By using a Markov partition, the system can be made to resemble a discrete-time Markov process
, with the long-term dynamical characteristics of the system represented as a Markov shift. The appellation 'Markov' is appropriate because the resulting dynamics of the system obeys the Markov property
. The Markov partition thus allows standard techniques from symbolic dynamics
to be applied, including the computation of expectation values, correlation
s, topological entropy
, topological zeta functions, Fredholm determinant
s and the like.
Suppose that M has been divided into a number of pieces E1,E2,…,Er, which are thought to be as small and localized, with virtually no overlaps. The behavior of a point x under the iterates of φ can be tracked by recording, for each n, the part Ei which contains φn(x). This results in an infinite sequence on the alphabet {1,2,…r} which encodes the point. In general, this encoding may be imprecise (the same sequence may represent many different points) and the set of sequences which arise in this way may be difficult to describe. Under certain conditions, which are made explicit in the rigorous definition of a Markov partition, the assignment of the sequence to a point of M becomes an almost one-to-one map whose image is a symbolic dynamical system of a special kind called a shift of finite type. In this case, the symbolic representation is a powerful tool for investigating the properties of the dynamical system (M,φ).
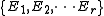such that
Here,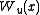
and 
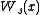are the unstable and stable manifold
s of x, respectively, and
simply denotes the interior of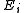 
.
These last two conditions can be understood as a statement of the Markov property
for the symbolic dynamics; that is, the movement of a trajectory from one open cover to the next is determined only by the most recent cover, and not the past history of the system. It is this property of the covering that merits the 'Markov' appellation. The resulting dynamics is that of a Markov shift; that this is indeed the case is due to theorems by Yakov Sinai (1968) and Rufus Bowen
(1975), thus putting symbolic dynamics on a firm footing.
Markov partitions make homoclinic and heteroclinic orbit
s particularly easy to describe.
Symbolic dynamics
In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
to be applied to the study of hyperbolic systems. By using a Markov partition, the system can be made to resemble a discrete-time Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
, with the long-term dynamical characteristics of the system represented as a Markov shift. The appellation 'Markov' is appropriate because the resulting dynamics of the system obeys the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
. The Markov partition thus allows standard techniques from symbolic dynamics
Symbolic dynamics
In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
to be applied, including the computation of expectation values, correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
s, topological entropy
Topological entropy
In mathematics, the topological entropy of a topological dynamical system is a nonnegative real number that measures the complexity of the system. Topological entropy was first introduced in 1965 by Adler, Konheim and McAndrew. Their definition was modelled after the definition of the...
, topological zeta functions, Fredholm determinant
Fredholm determinant
In mathematics, the Fredholm determinant is a complex-valued function which generalizes the determinant of a matrix. It is defined for bounded operators on a Hilbert space which differ from the identity operator by a trace-class operator...
s and the like.
Motivation
Let (M,φ) be a discrete dynamical system. A basic method of studying its dynamics is to find a symbolic representation: a faithful encoding of the points of M by sequences of symbols such that the map φ becomes the shift map.Suppose that M has been divided into a number of pieces E1,E2,…,Er, which are thought to be as small and localized, with virtually no overlaps. The behavior of a point x under the iterates of φ can be tracked by recording, for each n, the part Ei which contains φn(x). This results in an infinite sequence on the alphabet {1,2,…r} which encodes the point. In general, this encoding may be imprecise (the same sequence may represent many different points) and the set of sequences which arise in this way may be difficult to describe. Under certain conditions, which are made explicit in the rigorous definition of a Markov partition, the assignment of the sequence to a point of M becomes an almost one-to-one map whose image is a symbolic dynamical system of a special kind called a shift of finite type. In this case, the symbolic representation is a powerful tool for investigating the properties of the dynamical system (M,φ).
Formal definition
A Markov partition is a finite cover of the invariant set of the manifold by a set of curvilinear rectangles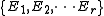 such that- For any pair of points
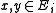, that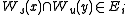 
-
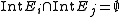for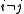 
- If
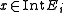and 
, then
Here,
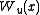and 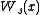are the unstable and stable manifoldStable manifold
In mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...
s of x, respectively, and
simply denotes the interior of 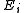.These last two conditions can be understood as a statement of the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
for the symbolic dynamics; that is, the movement of a trajectory from one open cover to the next is determined only by the most recent cover, and not the past history of the system. It is this property of the covering that merits the 'Markov' appellation. The resulting dynamics is that of a Markov shift; that this is indeed the case is due to theorems by Yakov Sinai (1968) and Rufus Bowen
Rufus Bowen
Robert Edward "Rufus" Bowen was an internationally known professor in the Department of Mathematics at the University of California, Berkeley, who specialized in dynamical systems theory...
(1975), thus putting symbolic dynamics on a firm footing.
Examples
Markov partitions have been constructed in several situations.- Anosov diffeomorphismAnosov diffeomorphismIn mathematics, more particularly in the fields of dynamical systems and geometric topology, an Anosov map on a manifold M is a certain type of mapping, from M to itself, with rather clearly marked local directions of 'expansion' and 'contraction'. Anosov systems are a special case of Axiom A...
s of the torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. - Dynamical billiardsDynamical billiardsA billiard is a dynamical system in which a particle alternates between motion in a straight line and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed...
, in which case the covering is countable.
Markov partitions make homoclinic and heteroclinic orbit
Heteroclinic orbit
In mathematics, in the phase portrait of a dynamical system, a heteroclinic orbit is a path in phase space which joins two different equilibrium points...
s particularly easy to describe.