Topological entropy
Encyclopedia
In mathematics
, the topological entropy of a topological dynamical system
is a nonnegative real number that measures the complexity of the system. Topological entropy was first introduced in 1965 by Adler, Konheim and McAndrew. Their definition was modelled after the definition of the Kolmogorov–Sinai, or metric, entropy. Later, Dinaburg and Rufus Bowen
gave a different, equivalent definition reminiscent of the Hausdorff dimension
. The second definition clarified the meaning of the topological entropy: for a system given by an iterated function
, the topological entropy represents the exponential growth rate of the number of distinguishable orbits of the iterates. An important variational principle relates the notions of topological and measure-theoretic entropy.
) and a continuous self-map f. Its topological entropy is a nonnegative real number that can be defined in various ways, which are known to be equivalent.
C of X, let H(C) be the logarithm
(usually to base 2) of the smallest number of elements of C that cover X. For two covers C and D, let
be their (minimal) common refinement, which consists of all the non-empty intersections of a set from C with a set from D, and similarly for multiple covers. For any continuous map f: X → X, the following limit exists:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the topological entropy of a topological dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
is a nonnegative real number that measures the complexity of the system. Topological entropy was first introduced in 1965 by Adler, Konheim and McAndrew. Their definition was modelled after the definition of the Kolmogorov–Sinai, or metric, entropy. Later, Dinaburg and Rufus Bowen
Rufus Bowen
Robert Edward "Rufus" Bowen was an internationally known professor in the Department of Mathematics at the University of California, Berkeley, who specialized in dynamical systems theory...
gave a different, equivalent definition reminiscent of the Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
. The second definition clarified the meaning of the topological entropy: for a system given by an iterated function
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
, the topological entropy represents the exponential growth rate of the number of distinguishable orbits of the iterates. An important variational principle relates the notions of topological and measure-theoretic entropy.
Definition
A topological dynamical system consists of a Hausdorff topological space X (usually assumed to be compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
) and a continuous self-map f. Its topological entropy is a nonnegative real number that can be defined in various ways, which are known to be equivalent.
Definition of Adler, Konheim, and McAndrew
Let X be a compact Hausdorff topological space. For any finite open coverCover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
C of X, let H(C) be the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
(usually to base 2) of the smallest number of elements of C that cover X. For two covers C and D, let
be their (minimal) common refinement, which consists of all the non-empty intersections of a set from C with a set from D, and similarly for multiple covers. For any continuous map f: X → X, the following limit exists:
-
Then the topological entropy of f, denoted h(f), is defined to be the supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of H(C, f) over all possible finite covers C of X.
Interpretation
The parts of C may be viewed as symbols that (partially) describe the position of a point x in X: all points x ∈ Ci are assigned the symbol Ci . Imagine that the position of x is (imperfectly) measured by a certain device and that each part of C corresponds to one possible outcome of the measurement. The integer
then represents the minimal number of "words" of length n needed to encode the points of X according to the behavior of their first n − 1 iterates under f, or, put differently, the total number of "scenarios" of the behavior of these iterates, as "seen" by the partition C. Thus the topological entropy is the average (per iteration) amount of informationInformationInformation in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
needed to describe long iterations of the map f.
Definition of Bowen and Dinaburg
This definition uses a metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on X (actually, uniform structure would suffice).
Let (X, d) be a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
and f: X → X be a continuous map. For each natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n, a new metric dn is defined on X by the formula
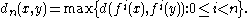
Given any ε > 0 and n ≥ 1, two points of X are ε-close with respect to this metric if their first n iterates are ε-close. This metric allows one to distinguish in a neighborhood of an orbit the points that move away from each other during the iteration from the points that travel together. A subset E of X is said to be (n, ε)-separated if each pair of distinct points of E is at least ε apart in the metric dn.
Denote by N(n, ε) the maximum cardinality of an (n, ε)-separated set. The topological entropy of the map f is defined by
Interpretation
Since X is compact, N(n, ε) is finite and represents the number of distinguishable orbit segments of length n, assuming that we cannot distinguish points within ε of one another. A straightforward argument shows that the limit defining h(f) always exists in the extended real line (but could be infinite). This limit may be interpreted as the measure of the average exponential growth of the number of distinguishable orbit segments. In this sense, it measures complexity of the topological dynamical system (X, f). Rufus Bowen extended this definition of topological entropy in a way which permits X to be noncompact.
See also
- Milnor–Thurston kneading theoryMilnor–Thurston kneading theoryThe Milnor–Thurston kneading theory is a mathematical theory which analyzes the iterates of piecewise monotone mappings of an interval into itself...
- For the measure of correlations in systems with topological orderTopological orderIn physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...
see Topological entanglement entropy
- Milnor–Thurston kneading theory