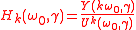Definition

The higher-order sinusoidal input describing functions (HOSIDF) were first introduced by dr. ir. P.W.J.M. Nuij. The HOSIDFs are an extension of the sinusoidal input describing function

Describing function

The Describing function method of Nikolay Mitrofanovich Krylov and Nikolay Bogolyubov is an approximate procedure for analyzing certain nonlinear control problems. It is based on quasi-linearization, which is the approximation of the non-linear system under investigation by an LTI system transfer...

 which describe the response (gain

Gain

In electronics, gain is a measure of the ability of a circuit to increase the power or amplitude of a signal from the input to the output. It is usually defined as the mean ratio of the signal output of a system to the signal input of the same system. It may also be defined on a logarithmic scale,...

 and phase

Phase (waves)

Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...

) of a system at harmonics of the base frequency of a sinusoidal input signal. The HOSIDFs bear an intuitive resemblance to the classical frequency response function and define the periodic output of a stable, causal

Causal system

A causal system is a system where the output depends on past/current inputs but not future inputs i.e...

, time invariant nonlinear system to a sinusoidal

Sine wave

The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...

input signal:



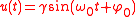
This output is denoted by and consists of harmonics of the input frequency: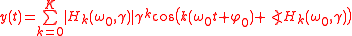



Defining the single sided spectra of the input and output as 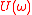and 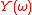, such that 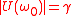yields the definition of the k-th order HOSIDF:

Advantages and applications

The application and analysis of the HOSIDFs is advantageous both when a nonlinear model is already identified and when no model is known yet. In the latter case the HOSIDFs require little model assumptions and can easily be identified while requiring no advanced mathematical tools. Moreover, even when a model is already identified, the analysis of the HOSIDFs often yields significant advantages over the use of the identified nonlinear model. First of all, the HOSIDFs are intuitive in their identification and interpretation while other nonlinear model structures often yield limited direct information about the behavior of the system in practice. Furthermore, the HOSIDFs provide a natural extension of the widely used sinusoidal describing functions in case nonlinearities cannot be neglected. In practice the HOSIDFs have two distinct applications: Due to their ease of identification, HOSIDFs provide a tool to provide on-site testing during system design. Finally, the application of HOSIDFs to (nonlinear) controller design for nonlinear systems is shown to yield significant advantages over conventional time domain based tuning.