Describing function
Encyclopedia
The Describing function method of Nikolay Mitrofanovich Krylov
and Nikolay Bogolyubov
is an approximate procedure for analyzing certain nonlinear control
problems. It is based on quasi-linearization, which is the approximation of the non-linear system under investigation by an LTI system transfer function
that depends on the amplitude
of the input waveform. By definition, a transfer function of a true LTI system cannot depend on the amplitude of the input function because an LTI system is linear
. Thus, this dependence on amplitude generates a family of linear systems that are combined in an attempt to capture salient features of the non-linear system behavior.
For example, consider when feedback is placed around a discontinuous (but piecewise continuous) nonlinearity (e.g., saturation
or deadband
effects) cascaded with a slow stable linear system. Depending on the amplitude of the output of the linear system, the feedback presented to the nonlinearity will be in a different continuous region. As the output of the linear system decays, the nonlinearity may move into a different continuous region. This switching from one continuous region to another can generate periodic oscillation
s. The describing function method attempts to predict characteristics of those oscillations (e.g., their fundamental frequency) by assuming that the slow system acts like a low-pass or bandpass filter that concentrates all energy around a single frequency. Even if the output waveform has several modes, the method can still provide intuition about properties like frequency and possibly amplitude; in this case, the describing function method can be thought of as describing the sliding mode
of the feedback system.
Using this low-pass assumption, the system response can be described by one of a family of sinusoidal waveform
s; in this case the system would be characterized by a sine input describing function (SIDF)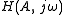
giving the system response to an input consisting of a sine wave of amplitude A and frequency 
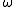. This SIDF is a modification of the transfer function
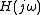used to characterize linear systems. In a quasi-linear system, when the input is a sine wave, the output will be a sine wave of the same frequency but with a scaled amplitude and shifted phase as given by 
. Many systems are approximately quasi-linear in the sense that although the response to a sine wave is not a pure sine wave, most of the energy in the output is indeed at the same frequency 
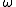as the input. This is because such systems may possess intrinsic low-pass or bandpass characteristics such that harmonics are naturally attenuated, or because external filter
s are added for this purpose. An important application of the SIDF technique is to estimate the oscillation amplitude in sinusoidal electronic oscillator
s.
Other types of describing functions that have been used are DFs for level inputs and for Gaussian noise inputs. Although not a complete description of the system, the DFs often suffice to answer specific questions about control and stability. DF methods are best for analyzing systems with relatively weak nonlinearities. In addition the higher order sinusoidal input describing function
s (HOSIDF), describe the response of a class of nonlinear systems at harmonics of the input frequency of a sinusoidal input. The HOSIDFs are an extension of the SIDF for systems where the nonlinearities are significant in the response.
or Kalman conjectures are fulfilled, there is no periodic solutions by describing function method, but counterexamples with periodic solutions are well known. Therefore, the application of describing function method requires additional justifications.
Nikolay Mitrofanovich Krylov
Nikolay Mitrofanovich Krylov was a Russian and Soviet mathematician known for works on interpolation, non-linear mechanics, and numerical methods for solving equations of mathematical physics.-Biography:...
and Nikolay Bogolyubov
Nikolay Bogolyubov
Nikolay Nikolaevich Bogolyubov was a Russian and Ukrainian Soviet mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and to the theory of dynamical systems; a recipient of the Dirac Prize...
is an approximate procedure for analyzing certain nonlinear control
Nonlinear control
Nonlinear control is the area of control engineering specifically involved with systems that are nonlinear, time-variant, or both. Many well-established analysis and design techniques exist for LTI systems ; however, one or both of the controller and the system under control in a general control...
problems. It is based on quasi-linearization, which is the approximation of the non-linear system under investigation by an LTI system transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
that depends on the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the input waveform. By definition, a transfer function of a true LTI system cannot depend on the amplitude of the input function because an LTI system is linear
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
. Thus, this dependence on amplitude generates a family of linear systems that are combined in an attempt to capture salient features of the non-linear system behavior.
For example, consider when feedback is placed around a discontinuous (but piecewise continuous) nonlinearity (e.g., saturation
Saturation
Saturation or saturated may refer to:- Meteorology :* Dew point, which is a temperature that occurs when atmospheric humidity reaches 100% and the air is saturated with moisture- Physics :...
or deadband
Deadband
A deadband is an area of a signal range or band where no action occurs . Deadband is used in voltage regulators and other controllers...
effects) cascaded with a slow stable linear system. Depending on the amplitude of the output of the linear system, the feedback presented to the nonlinearity will be in a different continuous region. As the output of the linear system decays, the nonlinearity may move into a different continuous region. This switching from one continuous region to another can generate periodic oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
s. The describing function method attempts to predict characteristics of those oscillations (e.g., their fundamental frequency) by assuming that the slow system acts like a low-pass or bandpass filter that concentrates all energy around a single frequency. Even if the output waveform has several modes, the method can still provide intuition about properties like frequency and possibly amplitude; in this case, the describing function method can be thought of as describing the sliding mode
Sliding mode control
In control theory, sliding mode control, or SMC, is a nonlinear control method that alters the dynamics of a nonlinear system by application of a discontinuous control signal that forces the system to "slide" along a cross-section of the system's normal behavior. The state-feedback control law is...
of the feedback system.
Using this low-pass assumption, the system response can be described by one of a family of sinusoidal waveform
Sine wave
The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
s; in this case the system would be characterized by a sine input describing function (SIDF)
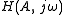giving the system response to an input consisting of a sine wave of amplitude A and frequency 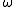. This SIDF is a modification of the transfer functionTransfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
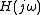used to characterize linear systems. In a quasi-linear system, when the input is a sine wave, the output will be a sine wave of the same frequency but with a scaled amplitude and shifted phase as given by . Many systems are approximately quasi-linear in the sense that although the response to a sine wave is not a pure sine wave, most of the energy in the output is indeed at the same frequency 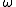as the input. This is because such systems may possess intrinsic low-pass or bandpass characteristics such that harmonics are naturally attenuated, or because external filterFilter (signal processing)
In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal...
s are added for this purpose. An important application of the SIDF technique is to estimate the oscillation amplitude in sinusoidal electronic oscillator
Electronic oscillator
An electronic oscillator is an electronic circuit that produces a repetitive electronic signal, often a sine wave or a square wave. They are widely used in innumerable electronic devices...
s.
Other types of describing functions that have been used are DFs for level inputs and for Gaussian noise inputs. Although not a complete description of the system, the DFs often suffice to answer specific questions about control and stability. DF methods are best for analyzing systems with relatively weak nonlinearities. In addition the higher order sinusoidal input describing function
Higher order sinusoidal input describing function
-Definition:The higher-order sinusoidal input describing functions were first introduced by . The HOSIDFs are an extension of the sinusoidal input describing function which describe the response of a system at harmonics of the base frequency of a sinusoidal input signal...
s (HOSIDF), describe the response of a class of nonlinear systems at harmonics of the input frequency of a sinusoidal input. The HOSIDFs are an extension of the SIDF for systems where the nonlinearities are significant in the response.
Caveats
Although describing function method may find oscillations for wide class of systems, it is well known that DF method can lead to incorrect results. Such examples have been presented by Tzypkin in a bang–bang systems. Also, in the case when conditions of Aizerman'sAizerman's conjecture
In nonlinear control, Aizerman's conjecture states that a linear system in feedback with a sector nonlinearity would be stable if the linear system is stable for any linear gain of the sector. This conjecture was proven false but led to the circle criterion and Popov criterion....
or Kalman conjectures are fulfilled, there is no periodic solutions by describing function method, but counterexamples with periodic solutions are well known. Therefore, the application of describing function method requires additional justifications.
Further reading
- Krylov N., and N. Bogolyubov: Introduction to Nonlinear Mechanics, Princeton University Press, 1947
- Gelb, A., and W. E. Vander Velde: Multiple-Input Describing Functions and Nonlinear System Design, McGraw Hill, 1968.
- P.W.J.M. Nuij, O.H. Bosgra, M. Steinbuch, Higher Order Sinusoidal Input Describing Functions for the Analysis of Nonlinear Systems with Harmonic Responses, Mechanical Systems and Signal Processing, 20(8), 1883–1904, (2006)