
Hilbert-Schmidt theorem
Encyclopedia
In mathematical analysis
, the Hilbert–Schmidt theorem, also known as the eigenfunction
expansion theorem, is a fundamental result concerning compact
, self-adjoint operator
s on Hilbert space
s. In the theory of partial differential equation
s, it is very useful in solving elliptic
boundary value problem
s.
or complex
Hilbert space and let A : H → H be a bounded, compact, self-adjoint operator. Then there is a sequence of non-zero real eigenvalues λi, i = 1, ..., N, with N equal to the rank
of A, such that |λi| is monotonically non-increasing and, if N = +∞,
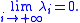
Furthermore, if each eigenvalue of A is repeated in the sequence according to its multiplicity
, then there exists an orthonormal set φi, i = 1, ..., N, of corresponding eigenfunctions, i.e.
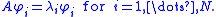
Moreover, the functions φi form an orthonormal basis
for the range
of A and A can be written as

Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, the Hilbert–Schmidt theorem, also known as the eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
expansion theorem, is a fundamental result concerning compact
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
, self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s. In the theory of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, it is very useful in solving elliptic
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s.
Statement of the theorem
Let (H, ⟨ , ⟩) be a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Hilbert space and let A : H → H be a bounded, compact, self-adjoint operator. Then there is a sequence of non-zero real eigenvalues λi, i = 1, ..., N, with N equal to the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of A, such that |λi| is monotonically non-increasing and, if N = +∞,
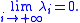
Furthermore, if each eigenvalue of A is repeated in the sequence according to its multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
, then there exists an orthonormal set φi, i = 1, ..., N, of corresponding eigenfunctions, i.e.
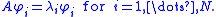
Moreover, the functions φi form an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
for the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of A and A can be written as


