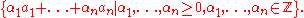Hilbert basis (linear programming)
Encyclopedia
In linear programming
, a Hilbert basis for a convex cone
C is an integer cone basis: minimal set of integer vectors such that every integer vector in C is a conical combination
of the vectors in the Hilbert basis with integer coefficients.
of integer vectors is a Hilbert basis if every integer vector in its convex cone
is also in its integer cone
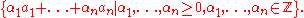
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
, a Hilbert basis for a convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
C is an integer cone basis: minimal set of integer vectors such that every integer vector in C is a conical combination
Conical combination
Given a finite number of vectors x_1, x_2, \dots, x_n\, in a real vector space, a conical combination or a conical sum of these vectors is a vector of the formwhere the real numbers \alpha_i\, satisfy \alpha_i\ge 0...
of the vectors in the Hilbert basis with integer coefficients.
Definition
A set of integer vectors is a Hilbert basis if every integer vector in its convex coneis also in its integer cone