Hill cipher
Encyclopedia
In classical cryptography, the Hill cipher is a polygraphic substitution cipher based on linear algebra
. Invented by Lester S. Hill
in 1929, it was the first polygraphic cipher in which it was practical (though barely) to operate on more than three symbols at once. The following discussion assumes an elementary knowledge of matrices
.
of n dimension
s, and multiplied by an n × n matrix
, modulo
26. (If one uses a larger number than 26 for the modular base, then a different number scheme can be used to encode the letters, and spaces or punctuation can also be used.) The whole matrix is considered the cipher key
, and should be random provided that the matrix is invertible in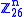
(to ensure decryption is possible). A Hill cipher is another way of working out the equation of a matrix.
Consider the message 'ACT', and the key below (or GYBNQKURP in letters):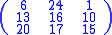
Since 'A' is 0, 'C' is 2 and 'T' is 19, the message is the vector: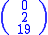
Thus the enciphered vector is given by: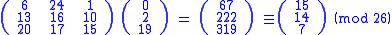
which corresponds to a ciphertext
of 'POH'. Now, suppose that our message is instead 'CAT', or:
This time, the enciphered vector is given by: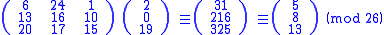
which corresponds to a ciphertext of 'FIN'. Every letter has changed. The Hill cipher has achieved Shannon
's diffusion
, and an n-dimensional Hill cipher can diffuse fully across n symbols at once.
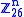the inverse matrix of the one in the previous example is: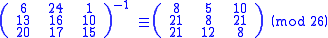
Taking the previous example ciphertext of 'POH', we get: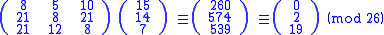
which gets us back to 'ACT', just as we hoped.
We have not yet discussed one complication that exists in picking the encrypting matrix. Not all matrices have an inverse (see invertible matrix). The matrix will have an inverse if and only if its determinant
is not zero, and does not have any common factors with the modular base. Thus, if we work modulo 26 as above, the determinant must be nonzero, and must not be divisible by 2 or 13. If the determinant is 0, or has common factors with the modular base, then the matrix cannot be used in the Hill cipher, and another matrix must be chosen (otherwise it will not be possible to decrypt). Fortunately, matrices which satisfy the conditions to be used in the Hill cipher are fairly common.
For our example key matrix:
So, modulo 26, the determinant is 25. Since this has no common factors with 26, this matrix can be used for the Hill cipher.
The risk of the determinant having common factors with the modulus can be eliminated by making the modulus prime
. Consequently a useful variant of the Hill cipher adds 3 extra symbols (such as a space, a period and a question mark) to increase the modulus to 29.
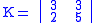
and suppose the plaintext message is HELP. Then this plaintext is represented by two pairs
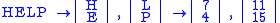
Then we compute
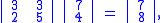
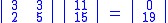
and continue encryption as follows:
The matrix K is invertible, hence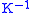
exists such that 
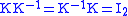. To implement decrypting, we compute
Then we compute
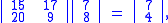
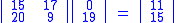
Therefore
.
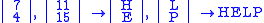because it is completely linear
. An opponent who intercepts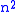
plaintext/ciphertext character pairs can set up a linear system which can (usually) be easily solved; if it happens that this system is indeterminate, it is only necessary to add a few more plaintext/ciphertext pairs. Calculating this solution by standard linear algebra algorithms then takes very little time.
While matrix multiplication alone does not result in a secure cipher it is still a useful step when combined with other non-linear operations, because matrix multiplication can provide diffusion
. For example, an appropriately chosen matrix can guarantee that small differences before the matrix multiplication will result in large differences after the matrix multiplication. Some modern ciphers use indeed a matrix multiplication step to provide diffusion. For example, the MixColumns step in AES
is a matrix multiplication. The function g in Twofish
is a combination of non-linear S-boxes with a carefully chosen matrix multiplication (MDS). Recently, some publications tried to make the Hill cipher secure.
is the binary logarithm
of the number of possible keys. There are
matrices of dimension n × n. Thus 
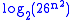or about 
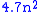is an upper bound on the key size of the Hill cipher using n × n matrices. This is only an upper bound because not every matrix is invertible and thus usable as a key. The number of invertible matrices can be computed via the Chinese Remainder Theorem
. I.e., a matrix is invertible modulo 26 if and only if it is invertible both modulo 2 and modulo 13.
The number of invertible n × n matrices modulo 2 is equal to the order of the general linear group
GL(n,Z2). It is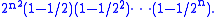
Equally, the number of invertible matrices modulo 13 (i.e. the order of GL(n,Z13)) is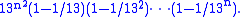
The number of invertible matrices modulo 26 is the product of those two numbers. Hence it is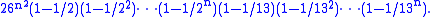
Additionally it seems to be prudent to avoid too many zeroes in the key matrix, since they reduce diffusion. The net effect is that the effective keyspace of a basic Hill cipher is about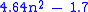
. For a 5 × 5 Hill cipher, that is about 114 bits. Of course, key search is not the most efficient known attack.
or the bifid cipher
, and in fact is weaker than either, and slightly more laborious to operate by pencil-and-paper. As the dimension increases, the cipher rapidly becomes infeasible for a human to operate by hand. A Hill cipher of dimension 6 was implemented mechanically. Hill and a partner were awarded a patent
for this device, which performed a 6 × 6 matrix multiplication modulo 26 using a system of gears and chains. Unfortunately the gearing arrangements (and thus the key) were fixed for any given machine, so triple encryption was recommended for security: a secret nonlinear step, followed by the wide diffusive step from the machine, followed by a third secret nonlinear step. Such a combination was actually very powerful for 1929, and indicates that Hill apparently understood the concepts of a meet-in-the-middle attack
as well as confusion and diffusion. Unfortunately, his machine did not sell.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
. Invented by Lester S. Hill
Lester S. Hill
Lester S. Hill was an American mathematician and educator who was interested in applications of mathematics to communications. He received a Bachelor's degree from Columbia College and a Ph.D. from Yale University . He taught at the University of Montana, Princeton University, the University of...
in 1929, it was the first polygraphic cipher in which it was practical (though barely) to operate on more than three symbols at once. The following discussion assumes an elementary knowledge of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
Operation
Each letter is first encoded as a number. Often the simplest scheme is used: A = 0, B =1, ..., Z=25, but this is not an essential feature of the cipher. A block of n letters is then considered as a vectorVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of n dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s, and multiplied by an n × n matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
26. (If one uses a larger number than 26 for the modular base, then a different number scheme can be used to encode the letters, and spaces or punctuation can also be used.) The whole matrix is considered the cipher key
Key (cryptography)
In cryptography, a key is a piece of information that determines the functional output of a cryptographic algorithm or cipher. Without a key, the algorithm would produce no useful result. In encryption, a key specifies the particular transformation of plaintext into ciphertext, or vice versa...
, and should be random provided that the matrix is invertible in
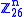(to ensure decryption is possible). A Hill cipher is another way of working out the equation of a matrix.Consider the message 'ACT', and the key below (or GYBNQKURP in letters):
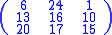
Since 'A' is 0, 'C' is 2 and 'T' is 19, the message is the vector:
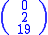
Thus the enciphered vector is given by:
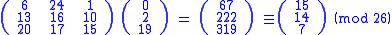
which corresponds to a ciphertext
Ciphertext
In cryptography, ciphertext is the result of encryption performed on plaintext using an algorithm, called a cipher. Ciphertext is also known as encrypted or encoded information because it contains a form of the original plaintext that is unreadable by a human or computer without the proper cipher...
of 'POH'. Now, suppose that our message is instead 'CAT', or:
This time, the enciphered vector is given by:
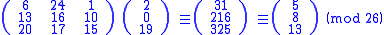
which corresponds to a ciphertext of 'FIN'. Every letter has changed. The Hill cipher has achieved Shannon
Claude Elwood Shannon
Claude Elwood Shannon was an American mathematician, electronic engineer, and cryptographer known as "the father of information theory"....
's diffusion
Confusion and diffusion
In cryptography, confusion and diffusion are two properties of the operation of a secure cipher which were identified by Claude Shannon in his paper Communication Theory of Secrecy Systems, published in 1949....
, and an n-dimensional Hill cipher can diffuse fully across n symbols at once.
Decryption
In order to decrypt, we turn the ciphertext back into a vector, then simply multiply by the inverse matrix of the key matrix (IFKVIVVMI in letters). (There are standard methods to calculate the inverse matrix; see matrix inversion for details.) We find that in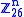 the inverse matrix of the one in the previous example is: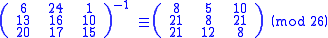Taking the previous example ciphertext of 'POH', we get:
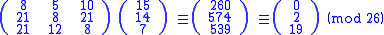
which gets us back to 'ACT', just as we hoped.
We have not yet discussed one complication that exists in picking the encrypting matrix. Not all matrices have an inverse (see invertible matrix). The matrix will have an inverse if and only if its determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is not zero, and does not have any common factors with the modular base. Thus, if we work modulo 26 as above, the determinant must be nonzero, and must not be divisible by 2 or 13. If the determinant is 0, or has common factors with the modular base, then the matrix cannot be used in the Hill cipher, and another matrix must be chosen (otherwise it will not be possible to decrypt). Fortunately, matrices which satisfy the conditions to be used in the Hill cipher are fairly common.
For our example key matrix:
So, modulo 26, the determinant is 25. Since this has no common factors with 26, this matrix can be used for the Hill cipher.
The risk of the determinant having common factors with the modulus can be eliminated by making the modulus prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. Consequently a useful variant of the Hill cipher adds 3 extra symbols (such as a space, a period and a question mark) to increase the modulus to 29.
Example
Let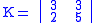and suppose the plaintext message is HELP. Then this plaintext is represented by two pairs
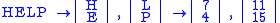
Then we compute
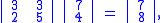
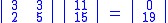
and continue encryption as follows:
The matrix K is invertible, hence
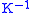exists such that 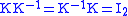. To implement decrypting, we computeThen we compute
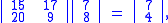
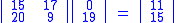
Therefore
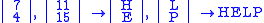.Security
Unfortunately, the basic Hill cipher is vulnerable to a known-plaintext attackKnown-plaintext attack
The known-plaintext attack is an attack model for cryptanalysis where the attacker has samples of both the plaintext , and its encrypted version . These can be used to reveal further secret information such as secret keys and code books...
because it is completely linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
. An opponent who intercepts
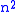plaintext/ciphertext character pairs can set up a linear system which can (usually) be easily solved; if it happens that this system is indeterminate, it is only necessary to add a few more plaintext/ciphertext pairs. Calculating this solution by standard linear algebra algorithms then takes very little time.While matrix multiplication alone does not result in a secure cipher it is still a useful step when combined with other non-linear operations, because matrix multiplication can provide diffusion
Confusion and diffusion
In cryptography, confusion and diffusion are two properties of the operation of a secure cipher which were identified by Claude Shannon in his paper Communication Theory of Secrecy Systems, published in 1949....
. For example, an appropriately chosen matrix can guarantee that small differences before the matrix multiplication will result in large differences after the matrix multiplication. Some modern ciphers use indeed a matrix multiplication step to provide diffusion. For example, the MixColumns step in AES
Advanced Encryption Standard
Advanced Encryption Standard is a specification for the encryption of electronic data. It has been adopted by the U.S. government and is now used worldwide. It supersedes DES...
is a matrix multiplication. The function g in Twofish
Twofish
In cryptography, Twofish is a symmetric key block cipher with a block size of 128 bits and key sizes up to 256 bits. It was one of the five finalists of the Advanced Encryption Standard contest, but was not selected for standardisation...
is a combination of non-linear S-boxes with a carefully chosen matrix multiplication (MDS). Recently, some publications tried to make the Hill cipher secure.
Key size
The key sizeKey size
In cryptography, key size or key length is the size measured in bits of the key used in a cryptographic algorithm . An algorithm's key length is distinct from its cryptographic security, which is a logarithmic measure of the fastest known computational attack on the algorithm, also measured in bits...
is the binary logarithm
Binary logarithm
In mathematics, the binary logarithm is the logarithm to the base 2. It is the inverse function of n ↦ 2n. The binary logarithm of n is the power to which the number 2 must be raised to obtain the value n. This makes the binary logarithm useful for anything involving powers of 2,...
of the number of possible keys. There are
matrices of dimension n × n. Thus 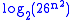or about 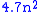is an upper bound on the key size of the Hill cipher using n × n matrices. This is only an upper bound because not every matrix is invertible and thus usable as a key. The number of invertible matrices can be computed via the Chinese Remainder TheoremChinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
. I.e., a matrix is invertible modulo 26 if and only if it is invertible both modulo 2 and modulo 13.
The number of invertible n × n matrices modulo 2 is equal to the order of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(n,Z2). It is
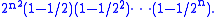
Equally, the number of invertible matrices modulo 13 (i.e. the order of GL(n,Z13)) is
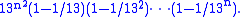
The number of invertible matrices modulo 26 is the product of those two numbers. Hence it is
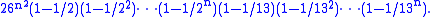
Additionally it seems to be prudent to avoid too many zeroes in the key matrix, since they reduce diffusion. The net effect is that the effective keyspace of a basic Hill cipher is about
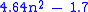. For a 5 × 5 Hill cipher, that is about 114 bits. Of course, key search is not the most efficient known attack.Mechanical implementation
When operating on 2 symbols at once, a Hill cipher offers no particular advantage over PlayfairPlayfair cipher
The Playfair cipher or Playfair square is a manual symmetric encryption technique and was the first literal digraph substitution cipher. The scheme was invented in 1854 by Charles Wheatstone, but bears the name of Lord Playfair who promoted the use of the cipher.The technique encrypts pairs of...
or the bifid cipher
Bifid cipher
In classical cryptography, the bifid cipher is a cipher which combines the Polybius square with transposition, and uses fractionation to achieve diffusion...
, and in fact is weaker than either, and slightly more laborious to operate by pencil-and-paper. As the dimension increases, the cipher rapidly becomes infeasible for a human to operate by hand. A Hill cipher of dimension 6 was implemented mechanically. Hill and a partner were awarded a patent
Patent
A patent is a form of intellectual property. It consists of a set of exclusive rights granted by a sovereign state to an inventor or their assignee for a limited period of time in exchange for the public disclosure of an invention....
for this device, which performed a 6 × 6 matrix multiplication modulo 26 using a system of gears and chains. Unfortunately the gearing arrangements (and thus the key) were fixed for any given machine, so triple encryption was recommended for security: a secret nonlinear step, followed by the wide diffusive step from the machine, followed by a third secret nonlinear step. Such a combination was actually very powerful for 1929, and indicates that Hill apparently understood the concepts of a meet-in-the-middle attack
Meet-in-the-middle attack
The meet-in-the-middle attack is a cryptographic attack which, like the birthday attack, makes use of a space-time tradeoff. While the birthday attack attempts to find two values in the domain of a function that map to the same value in its range, the meet-in-the-middle attack attempts to find a...
as well as confusion and diffusion. Unfortunately, his machine did not sell.
See also
Other practical "pencil-and-paper" polygraphic ciphers include:- Playfair cipherPlayfair cipherThe Playfair cipher or Playfair square is a manual symmetric encryption technique and was the first literal digraph substitution cipher. The scheme was invented in 1854 by Charles Wheatstone, but bears the name of Lord Playfair who promoted the use of the cipher.The technique encrypts pairs of...
- Bifid cipherBifid cipherIn classical cryptography, the bifid cipher is a cipher which combines the Polybius square with transposition, and uses fractionation to achieve diffusion...
- Trifid cipherTrifid cipherIn classical cryptography, the trifid cipher is a cipher invented around 1901 by Felix Delastelle, which extends the concept of the bifid cipher to a third dimension, allowing each symbol to be fractionated into 3 elements instead of two...
External links
- "Hill Cipher Web App" implements the Hill cipher and shows the matrices involved
- "Hill Cipher Explained" illustrates the linear algebra behind the Hill Cipher
- "Hill Cipher Deciphered" provides an excellent explanation of computing matrix inverses with regard to the Hill cipher.