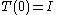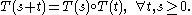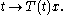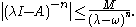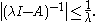Hille–Yosida theorem
Encyclopedia
In functional analysis
, the Hille–Yosida theorem characterizes the generators of strongly continuous one-parameter semigroup
s of linear operators on Banach space
s. It is sometimes stated for the special case of contraction semigroups, with the general case being called the Feller–Miyadera–Phillips theorem (after William Feller
, Ryohei Miyadera, and Ralph Phillips). The contraction semigroup case is widely used in the theory of Markov process
es. In other scenarios, the closely related Lumer–Phillips theorem is often more useful in determining whether a given operator generates a strongly continuous contraction semigroup. The theorem is named after the mathematician
s Einar Hille and Kosaku Yosida
who independently discovered the result around 1948.
{T(t)} t ∈[0, ∞) such that
The semigroup is said to be strongly continuous, also called a (C0) semigroup, if and only if the mapping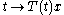
is continuous for all x ∈ X, where[0, ∞) has the usual topology and X has the norm topology.
The infinitesimal generator of a one-parameter semigroup T is an operator A defined on a possibly proper subspace of X as follows:
The infinitesimal generator of a strongly continuous one-parameter semigroup is a closed linear operator defined on a dense linear subspace
of X.
The Hille–Yosida theorem provides a necessary and sufficient condition for a closed linear operator A on a Banach space to be the infinitesimal generator of a strongly continuous one-parameter semigroup.
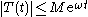if and only if
Let A be a linear operator defined on a linear subspace D(A) of the Banach space
X. Then A generates a contraction semigroup if and only if
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the Hille–Yosida theorem characterizes the generators of strongly continuous one-parameter semigroup
C0-semigroup
In mathematics, a C0-semigroup, also known as a strongly continuous one-parameter semigroup, is a generalization of the exponential function...
s of linear operators on Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. It is sometimes stated for the special case of contraction semigroups, with the general case being called the Feller–Miyadera–Phillips theorem (after William Feller
William Feller
William Feller born Vilibald Srećko Feller , was a Croatian-American mathematician specializing in probability theory.-Early life and education:...
, Ryohei Miyadera, and Ralph Phillips). The contraction semigroup case is widely used in the theory of Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
es. In other scenarios, the closely related Lumer–Phillips theorem is often more useful in determining whether a given operator generates a strongly continuous contraction semigroup. The theorem is named after the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s Einar Hille and Kosaku Yosida
Kosaku Yosida
was a Japanese mathematician who worked in the field of functional analysis. He is known for the Hille-Yosida theorem concerning C0-semigroups.- References :...
who independently discovered the result around 1948.
Formal definitions
If X is a Banach space, a one-parameter semigroup of operators on X is a family of operators indexed on the non-negative real numbers{T(t)} t ∈
The semigroup is said to be strongly continuous, also called a (C0) semigroup, if and only if the mapping
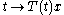
is continuous for all x ∈ X, where
The infinitesimal generator of a one-parameter semigroup T is an operator A defined on a possibly proper subspace of X as follows:
- The domain of A is the set of x ∈ X such that
-
-
- has a limit as h approaches 0 from the right.
- The value of A x is the value of the above limit. In other words A x is the right-derivative at 0 of the function
The infinitesimal generator of a strongly continuous one-parameter semigroup is a closed linear operator defined on a dense linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of X.
The Hille–Yosida theorem provides a necessary and sufficient condition for a closed linear operator A on a Banach space to be the infinitesimal generator of a strongly continuous one-parameter semigroup.
Statement of the theorem
Let A be a linear operator defined on a linear subspace D(A) of the Banach space X, ω a real number, and M > 0. Then A generates a strongly continuous semigroup T that satisfies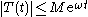 if and only if
- D(A) is dense in X, and
- every real λ > ω belongs to the resolvent setResolvent setIn linear algebra and operator theory, the resolvent set of a linear operator is a set of complex numbers for which the operator is in some sense "well-behaved". The resolvent set plays an important role in the resolvent formalism.-Definitions:...
of A and for such λ and for all positive integers n
Hille-Yosida theorem for contraction semigroups
In the general case the Hille–Yosida theorem is mainly of theoretical importance since the estimates on the powers of the resolvent operator that appear in the statement of the theorem can usually not be checked in concrete examples. In the special case of contraction semigroups (M = 1 and ω = 0 in the above theorem) only the case n = 1 has to be checked and the theorem also becomes of some practical importance. The explicit statement of the Hille–Yosida theorem for contraction semigroups is:Let A be a linear operator defined on a linear subspace D(A) of the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
X. Then A generates a contraction semigroup if and only if
- D(A) is dense in X, and
- every real λ > 0 belongs to the resolvent set of A and for such λ
See also
- C0 semigroup
- Lumer–Phillips theorem
- Stone's theorem on one-parameter unitary groupsStone's theorem on one-parameter unitary groupsIn mathematics, Stone's theorem on one-parameter unitary groups is a basic theorem of functional analysis which establishes a one-to-one correspondence between self-adjoint operators on a Hilbert space H and one-parameter families of unitary operators...