
Resolvent set
Encyclopedia
In linear algebra
and operator theory
, the resolvent set of a linear operator is a set of complex number
s for which the operator is in some sense "well-behaved
". The resolvent set plays an important role in the resolvent formalism
.
and let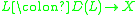 be a linear operator with domain
be a linear operator with domain
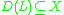 . Let id denote the identity operator
. Let id denote the identity operator
on X. For any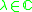 , let
, let
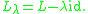
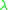 is said to be a regular value if
is said to be a regular value if 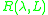 , the inverse operator
, the inverse operator
to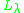
The resolvent set of L is the set of all regular values of L:

The spectrum
is the complement
of the resolvent set:
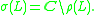
The spectrum can be further decomposed into the point/discrete spectrum (where condition 1 fails), the continuous spectrum (where conditions 1 and 3 hold but condition 2 fails) and the residual/compression spectrum (where condition 1 holds but condition 3 fails).
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, the resolvent set of a linear operator is a set of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s for which the operator is in some sense "well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
". The resolvent set plays an important role in the resolvent formalism
Resolvent formalism
In mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
.
Definitions
Let X be a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
and let
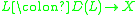 be a linear operator with domain
be a linear operator with domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
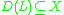 . Let id denote the identity operator
. Let id denote the identity operatorIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on X. For any
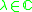 , let
, let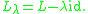
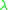 is said to be a regular value if
is said to be a regular value if 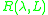 , the inverse operator
, the inverse operatorInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
to
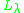
- exists;
- is a bounded linear operator;
- is defined on a denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
subspace of X.
The resolvent set of L is the set of all regular values of L:

The spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
is the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the resolvent set:
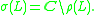
The spectrum can be further decomposed into the point/discrete spectrum (where condition 1 fails), the continuous spectrum (where conditions 1 and 3 hold but condition 2 fails) and the residual/compression spectrum (where condition 1 holds but condition 3 fails).
Properties
- The resolvent set
 of a bounded linear operator L is an open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of a bounded linear operator L is an open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
.

